Ähnlichkeitssatz für Dreiecke

Question

Liebe Forum-Mitglieder,

Aufgabe:

…

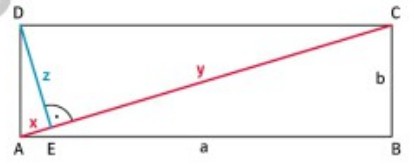
a) Zeige, dass das Rechteck ABCD in drei ähnliche Dreiecke zerlegt worden ist.

b) Begründe: "In einem Rechteck ABCD teilt das Lot von D auf die Diagonale AC die Diagonale im Verhältnis b²:a²."

Problem/Ansatz:

a) Um zu bergünden, dass die Dreiecke ähnlich sind, müsste ich die beiden Ähnlichkeitssätze für Dreiecke anwenden (WW-Satz; S:S:S-Satz). Aber ich kann doch für alle Figuren nur sagen, dass sie einen rechten Winkel haben und in jeweils einer Seite übereinstimmen. Dies erfüllt er aber keines der beiden Ähnlichkeitssätze. Gibt es noch eine andere Größe/ Länge, die man herausfinden kann?

LG

Orbi

Answer 1

Aber ich kann doch für alle Figuren nur sagen, dass sie einen rechten Winkel haben

Wie wäre es zusätzlich mit Wechselwinkeln an geschnittenen Parallelen?

Oder mit dem gemeinsamen Innenwinkel der Dreiecke ACD und HCD? (Mit H bezeichne ich den Fußpunkt der eingezeichneten Höhe.)

Oder mit Innnenwinkeln, die die gemeinsame Größe 90°-∠BAC haben?

Answer 2

Du musst nur zeigen, dass jeweils zwei Winkel gleich sind. Die Seitenlängen spielen keine Rolle.

Alle Dreiecke sind rechtwinklig.

Nun musst du nur noch erläutern, warum die kleineren spitzen Winkel alle gleich groß sind.

:-)

Comments

oder die größeren...

;-)

---

Ich wollte es nicht zu kompliziert machen...

:-)