Steckbriefaufgabe lösen?

Question

Aufgabe:

Für eine Spielzeug-Eisenbahnbrücke müssen gebo-
gene Schienen produziert werden. Für die maschinel-
le Herstellung soll die Form dieser Schienen durch
eine ganzrationale beschrieben werden.
a.) Ermitteln Sie mithilfe Ihres GTRs eine ganzratio-
nale Funktion 3. Grades, deren Graph den Verlauf der Schiene modelliert.
b.) Zeigen Sie, dass die Schiene waagerecht am Boden abschließt.
c.) Berechnen Sie, wie groß das größte Gefälle (Steigung) in der Mitte der Schiene

Problem/Ansatz:

ich verstehe die Aufgabe nicht:(

Answer 1

Nutze http://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm zur Hilfe und Selbstkontrolle

Eigenschaften

f(0)=7
f'(0)=0
f(20)=0
f'(20)=0

Gleichungssystem

d = 7
c = 0
8000a + 400b + 20c + d = 0
1200a + 40b + c = 0

Errechnete Funktion

f(x) = 7/4000·x^3 - 0,0525·x^2 + 7

Comments

b) Zeigen Sie, dass die Schiene waagerecht am Boden abschließt.

Eigentlich finde ich die Aufgabe etwas quatsch, weil man die Bedingungen letztendlich bereits bei a) verwendet hat. Und ich glaube nicht das man die verwendet ohne zu wissen was es bedeutet.

---

Wie kommst du auf die Funktion ?

---

Zunächst mal stellt man die Eigenschaften auf. Aus diesen Eigenschaften entwickelt man die Gleichungen und das entstehende Gleichungssystem muss man dann lösen. Es sind also drei Schritte die du bis zur Funktion machen musst.

---

Wie kommst du auf die Funktion ?

Grundsätzlich weiß ich nicht wie man bei der Aufgabe a auf die gleichung zu kommen

---

f(0)=7
f'(0)=0
f(20)=0
f'(20)=0

f ( x ) = a*x^3 + b * x^2 + c * x + d
f ´( x ) = 3a*x^2 + 2b * x + c

Einsetzen
f ( 0 ) = a * 0^3 + b * 0 + c * 0 + d = 7
d = 7
f '(0) = 0
f ´( 0 ) = 3a*0^2 + 2b * 0 + c = 0
c = 0

d und c schon einmal eingesetzt
f ( x ) = a*x^3 + b * x^2 + 7
f ´( x ) = 3a*x^2 + 2b * x

f ( 20 ) = a * 20^3 + b * 20^2 + 7 = 0
f ´ ( 20 ) = 3 * a * 20^2 + 2 * b * 20 =0

a * 20^3 + b * 20^2 + 7 = 0
3 * a * 20^2 + 2 * b * 20 =0

Schaffst du den Rest ?

Answer 2

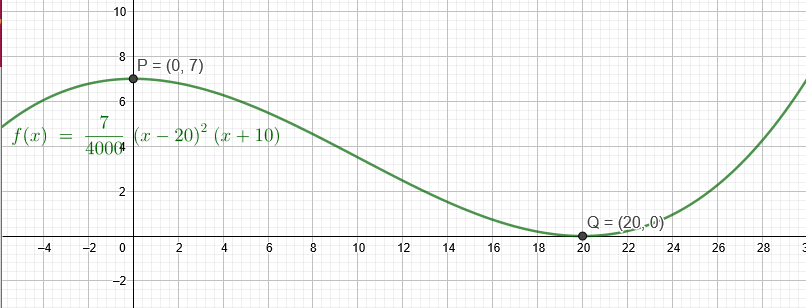
P(0|7) Maximum, waagerechte Tangente

Q(20|0)Minimum , waagerechte Tangente (doppelte Nullstelle)

Lösung über Nullstellenform der Parabel 3.Grades:

\(f(x)=a*(x-20)^2*(x-N)\)

\(P(0|7)\)

\(f(0)=a*(0-20)^2*(0-N)=-400a*N\)

\(-400a*N=7→a=-\frac{7}{400N}\)

Extremwerteigenschaft (waagerechte Tangente)

\(f´(x)=-\frac{7}{400N}*[(2x-40)*(x-N)+(x-20)^2*1\)]

\(f´(0)=-\frac{7}{400N}*[40N+400]\)]

\(-\frac{7}{400N}*[40N+400]=0→N=-10\)]

\(a=-\frac{7}{400*(-10}=\frac{7}{4000}\)

\(f(x)=\frac{7}{4000}*(x-20)^2*(x+10)\)