Bestimme Eigenwerte und Eigenvektoren von A und gib die Diagonalisierung von A an.

Question

Aufgabe:

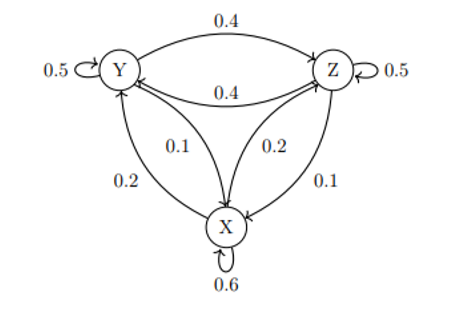
Gegeben ist die folgende Markow-Kette mit den drei Zuständen \( X, Y \) und \( Z \) :

a) Bestimme Eigenwerte und Eigenvektoren von \( A \) und gib die Diagonalisierung von \( A \) an.

Eigenwerte sind 1/2,1, 1/10

Vektoren sind -2/1/1, 1/2/2, 0/-1/1

Problem/Ansatz:

Weiß jemand wie man die Diagonalisierung ausrechnet?

Answer 1

Mit Deinen EVs kommst Du nicht zurecht:

guckst Du https://www.geogebra.org/m/upUZg79r

\(\small \left(\begin{array}{rrrr}\lambda=&\frac{1}{10}&\left(\begin{array}{rrr}\frac{1}{2}&\frac{1}{5}&\frac{1}{5}\\\frac{1}{10}&\frac{2}{5}&\frac{2}{5}\\\frac{1}{10}&\frac{2}{5}&\frac{2}{5}\\\end{array}\right)&\left(\begin{array}{r}x1\\x2\\x3\\\end{array}\right) = 0\\\lambda=&\frac{1}{2}&\left(\begin{array}{rrr}\frac{1}{10}&\frac{1}{5}&\frac{1}{5}\\\frac{1}{10}&0&\frac{2}{5}\\\frac{1}{10}&\frac{2}{5}&0\\\end{array}\right)&\left(\begin{array}{r}x1\\x2\\x3\\\end{array}\right) = 0\\\lambda=&1&\left(\begin{array}{rrr}\frac{-2}{5}&\frac{1}{5}&\frac{1}{5}\\\frac{1}{10}&\frac{-1}{2}&\frac{2}{5}\\\frac{1}{10}&\frac{2}{5}&\frac{-1}{2}\\\end{array}\right)&\left(\begin{array}{r}x1\\x2\\x3\\\end{array}\right) = 0\\\end{array}\right)\)

==> EV

\(\small T \, :=  \, \left(\begin{array}{rrr}0&-4&1\\-1&1&1\\1&1&1\\\end{array}\right)\)

\(\small T^{-1} A \, T :=  \, \left(\begin{array}{rrr}\frac{1}{10}&0&0\\0&\frac{1}{2}&0\\0&0&1\\\end{array}\right)\)