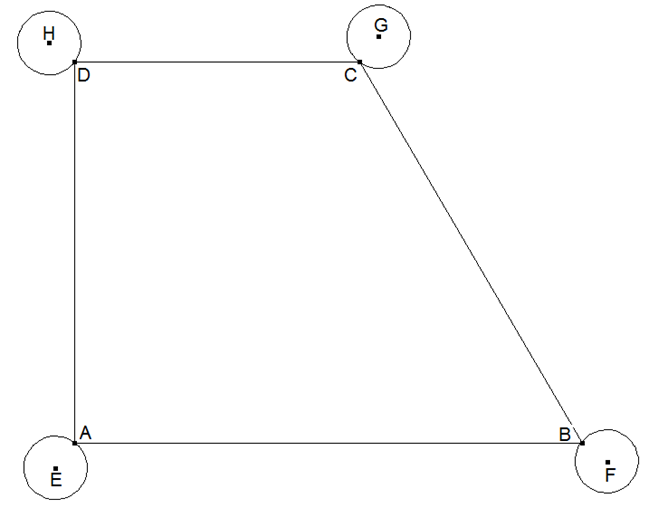
Ein trapezförmiger Teich hat im Koordinatensystem (LE=1 m) die Ecken A(0|0), B(16|0), C(9|12) und D(0|12). In den Positionen E(-0,6|-0,8), F(16,8|-0,6), G(9,6|12,8) und H(-0,8|12,6) wachsen schützenswerte Bäume, deren Wurzelteller (Radius je 1m) nicht verletzt werden darf. Kann man die Teichfläche auf das Doppelte vergrößern, sodass sie viereckig bleibt, ohne gegen Naturschutzauflagen zu verstoßen?