Liebe Lounge,
ich möchte folgenden Satz beweisen:
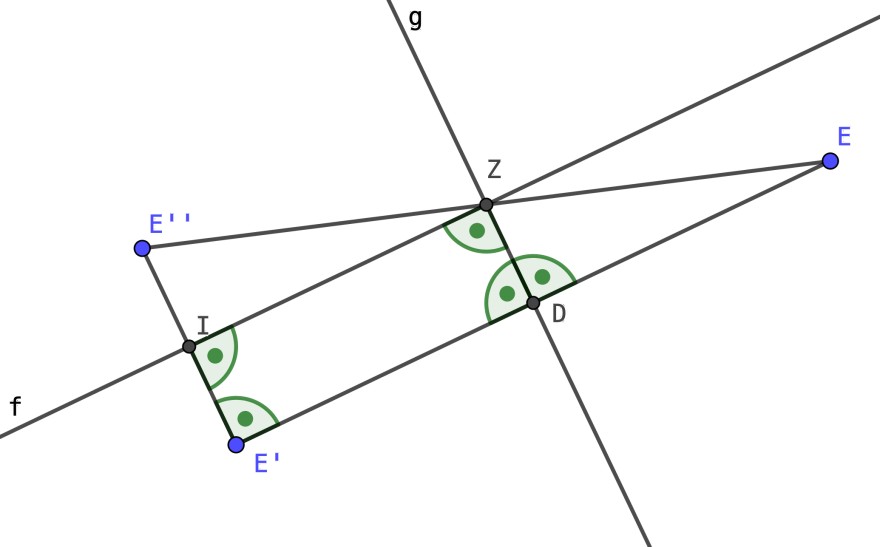
Seien g und f zwei zueinander senkrechte Geraden, die sich im Punkt Z schneiden.
Figur A wird nun zunächst an g und dann an f gespiegelt. Dann ist die entstandene Figur A'' punktsymmetrisch zu A, das Symmetriezentrum ist Punkt Z.
Beweis: Sei E ein Eckpunkt der Figur A. Durch Spiegelung an g entsteht E'. Es gilt ED=E'D, EDZ=90° und ZDE'=90°. Durch Spiegelung von E' an f entsteht E''. Es gilt: E'I=E''I, E'IZ=90° und ZIE''=90°.
Das Viereck DZIE' ist ein Rechteck (muss das extra gezeigt werden?). Es gilt demnach: ED=E'D=ZI. Zudem gilt ZD=IE'=IE''. Somit sind die Dreiecke EZD und ZE''I nach SWS kongruent. Insbesondere gilt dadurch: EZ=E''Z, womit die Aussage beweisen wäre.
Der Beweis für mögliche andere Eckpunkt der Figur A folgt identisch.
Reicht das so? Oder muss ich noch Zeigen, dass Z tatsächlich auf der Strecke EE'' liegt?
!!