Extremwerte: Gegeben sei die Funktion\( f(x)=x^{3}+b*x-b \)mit einem reellen Parameter \( b \).
a) Für welche Werte von \( b \) hat die Funktion an der Stelle \( x=-1 \) ein Extremum?
\( f´(x)=3*x^{2}+b\)
\( f´(-1)=3+b→3+b=0→b=-3\)
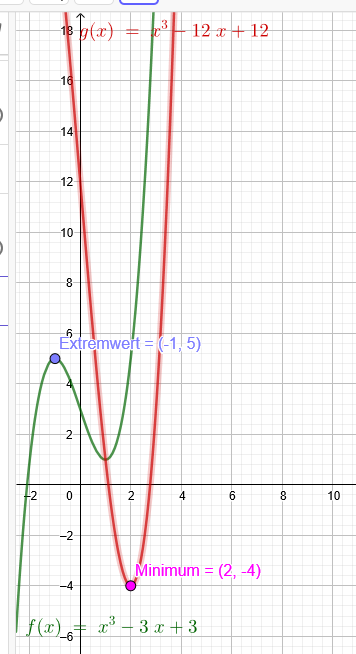
\( f(x)=x^{3}-3*x+3 \)
b) Gibt es einen Wert \( b \), so dass die Funktion in \( x=-2 \) ein Minimum hat?
\( f´(x)=3*x^{2}+b\)
\( f´(-2)=12+b→12+b=0→b=-12\)
\( f(x)=x^{3}-12*x+12 \)