Hallo,
Berechne den Schwerpunkt eines Viertelkreises und ziehe diesen gewichtet vom Schwerpunkt des Kreises (dem Mittelpunkt) ab. Im Detail geht das so:
Ein Viertelkreis mit Radius \(r\) ist modelliert durch die Funktion$$k(x) = \sqrt{r^2-x^2} \quad x \in [0\dots r]$$die übliche Schwerpunktberechnung ...$$\begin{aligned} x_s &= \frac1{F_{vk}}\int\limits_{x=0}^{r} xk(x)\,\text dx \\ &= \frac4{r^2 \pi}\int\limits_{x=0}^{r} x\sqrt{r^2-x^2} \,\text dx \\ &= \frac4{r^2 \pi} \left[-\frac13\left(r^2-x^2\right)^{\frac32}\right]_{x=0}^r \\ &= \frac4{r^2 \pi} \cdot \frac13 r^3 \\ x_s&= \frac4{3\pi} r \\ \end{aligned}$$Wegen der Symmetrie des Viertelkreises ist der Y-Wert identisch zum X-Wert. Also ist seine Entfernung \(r_s\) vom Mittelpunkt (auf der Symmetrieachse)$$r_s = \sqrt 2 \cdot x_s = \frac{4\sqrt 2}{3\pi} r$$Da sich die Fläche des Dreiviertelkreises zum Viertelkreises wie \(3:1\) verhält, liegt der Schwerpunkt des Dreiviertelkreises bei $$s = \frac13 r_s = \frac{4\sqrt 2}{9\pi} r \approx 0,20007\, r$$
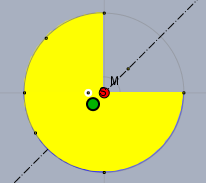
Der Schwerpunkt (grün) liegt also ca. bei \(0,2\,r\) vom Mittelpunkt entfernt auf der Symmetrieachse.
Gruß Werner