Die Holzbretter, die Wasserrinne und der Querschnitt

Question

Aufgabe:

Aus drei Holzbrettern von je 20 cm Breite soll eine Wasserrinne von trapezförmigem Querschnitt mit möglichst großem Fassungsvermögen gebaut werden. Geben Sie eine genaue Konstruktionsanweisung!

Problem/Ansatz:

hat jemand eine Lösung mit Lösungsweg für mich? Vielen Dank im Voraus. Ich habe nämlich keine Ahnung wie ich das lösen soll.

Answer 1

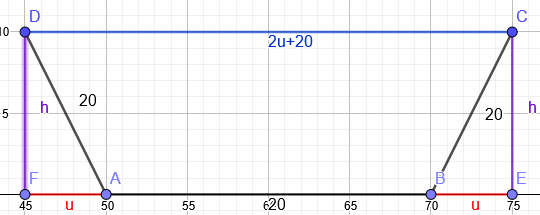
"Aus drei Holzbrettern von je 20 cm Breite soll eine Wasserrinne von trapezförmigem Querschnitt mit möglichst großem Fassungsvermögen gebaut werden. Geben Sie eine genaue Konstruktionsanweisung!"

\(A=\frac{a+c}{2}*h\) soll maximal werden.

\(a=20  und c=20+2u\)

\(A(u,h)=\frac{20+20+2u}{2}*h=(20+u)*h\)

\(h^2+u^2=20^2→h=\sqrt{400-u^2}\)

\(A(u)=(20+u)*\sqrt{400-u^2}\)

\(A´(u)=1*\sqrt{400-u^2}+\frac{(20+u)*(-2u)}{2*\sqrt{400-u^2}}\)

\(A´(u)=\sqrt{400-u^2}-\frac{(20u+u^2)}{\sqrt{400-u^2}}\)

\(\sqrt{400-u^2}-\frac{(20u+u^2)}{\sqrt{400-u^2}}=0\)

\((400-u^2)-(20u+u^2)=0\)

\(u^2+10u=200\)

\((u+5)^2=200+25=225|\sqrt{}\)

1.) \(u+5=15\)

\(u₁=10\)

2.) \(u+5=-15\)

\(u₂=-20\) entfällt

\(h=\sqrt{400-100}=\sqrt{300}\)

Comments

Die seitlichen Bretter sollen doch aber auch 20 cm breit sein...

---

Das stimmt. In der Zeichnung ist nur a=20 dargestellt.

---

Ich befürchte, ich verstehe diese Zeichnung immer noch nicht. Du schreibst u = 10 und zeichnest u = 5, und Du schreibst h = \( \sqrt{300} \) und zeichnest h = 10 ?

---

Diese Zeichnung ist nur eine Skizze zum Verstehen. Vielleicht kommt es so rüber, dass in der Zeichnung die ausgerechneten Werte zu sehen sind. So ist es aber nicht.

---

Eine Skizze soll dazu dienen sich die Rechnungen zu überlegen bzw. den rechnerischen Hintergrund zu verstehen.

Wenn die Zeichnung vor der Rechnung gemacht wird, wie es sein sollte, dann braucht sie nicht maßstabsgetreu sein und natürlich auch nicht die Lösungen enthalten, die man zu diesem Zeitpunkt noch nicht kennt.

---

Danke! Werde ich Zukunft so machen.

Answer 2

Maximiere den Flächeninhalt des Trapezes.

Flächeninhalt = 1/2 * (untere Kante + obere Kante) * Höhe

Comments

Der Querschnitt:

alle Längenangaben in Zentimeter:

untere Kante: 20

obere Kante: \( \sqrt{20^2 - h^2}  + 20 + \sqrt{20^2 - h^2} \)

Höhe: h

Flächeninhalt: A(h) = 1/2 * (20 + \( \sqrt{20^2 - h^2}  + 20 + \sqrt{20^2 - h^2} \)) * h

erste Ableitung = Null setzen   ⇒   h = \( \sqrt{300} \)