die notwendige Bedingung für einen Hochpunkt des Graphen der Funktion f(x) ist, dass deren erste Ableitung = 0 ist.
Die hinreichende Bedingung ist dann, dass die zweite Ableitung von f(x) < 0 ist.
Die notwendige Bedingung für einen Tiefpunkt des Graphen der Funktion f(x) ist ebenfalls, dass deren erste Ableitung = 0 ist. Die hinreichende Bedingung ist dann, dass die zweite Ableitung von f(x) > 0 ist.
Wir berechnen also zunächst einmal die 1. und die 2. Ableitung:
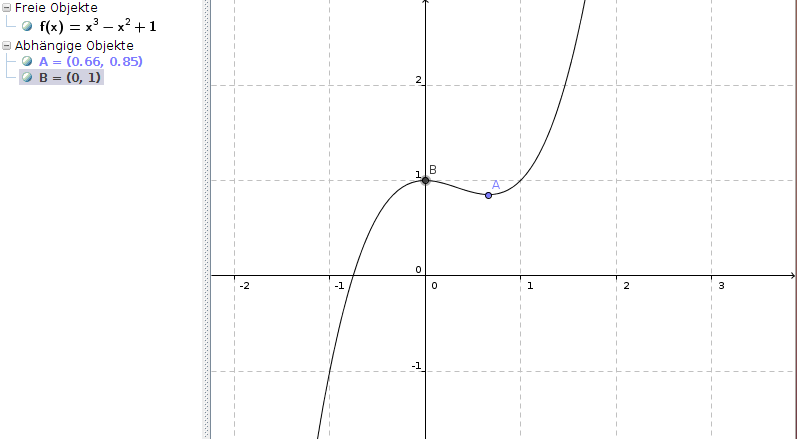
f(x) = x3 - x2 + 1
f'(x) = 3x2 - 2x
f''(x) = 6x - 2
3x2 - 2x = 0
x * (3x - 2) = 0
x1 = 0
3x - 2 = 0
x2 = 2/3
Jetzt beides zur Überprüfung in f''(x) eingesetzt:
f''(0) = 6 * 0 - 2 = -2 < 0, also Hochpunkt (B) an (0|f(0)) = (0|1)
f''(2/3) = 6 * 2/3 - 2 = 4 - 2 = 2 > 0, also Tiefpunkt (A) an (2/3|f(2/3)) = (2/3|8/27 - 4/9 + 1) = (2/3|8/27 - 12/27 + 27/27) =
(2/3| 23/27)
Besten Gruß