Ist die Negation so richtig?

Question

Folgende Aufgabe:

Es gilt diese Aussage zu beweisen.

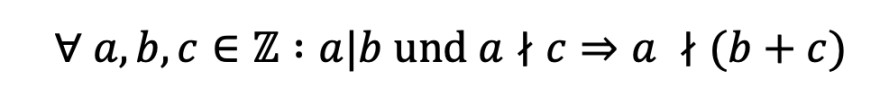
Text erkannt:

\( \forall a, b, c \in \mathbb{Z}: a \mid b \) und \( a \nmid c \Rightarrow a \nmid(b+c) \)

Mein Vorschlag:

Mit einem indirekten Beweis (Widerspruchsbeweis)

Dazu will ich als erstes die Negation der Aussage bilden.

Ist das so richtig?:

∃ a,b,c ∈ ℤ: a|b ∨ a|c ⇒ a | (b+c)

Ist die Negation so richtig?

Gesetz der Teilbarkeit: ∀ a,b ∈ ℤ: (a|b ⇔ ∃k∈ℤ : a*k = b)

aus a|b ∨ a|c ⇒ a | (b+c) wird also a*k = b ∧ a*l = c ⇒ a*m = b+c

spätestens jetzt glaube ich, dass meine Negation falsch ist und weiter komme ich leider auch nicht

Kann mir vielleicht jemand helfen bitte?

Answer 1

Die Negation ist:

\(\exists a,b,c \in \mathbb{Z}:\; a|b\, \wedge\;  a\not | c\; \wedge \;  a|(b+c)\)

und dass dies nicht der Fall ist, kannst du leicht zeigen.

Comments

Wie kann ich das denn leicht zeigen? Ich muss ja irgendwo einen Widerspruch bewirken, aber wo finde ich den?

Ich kann a|b schreiben als a*k = b

a ist nicht Teiler von c als a*l ≠ c

Liegt der Widerspruch darin, dass a|(b+c) nicht angenommen werden darf, weil c ungleich a*l ist oder wie soll ich das verstehen?

---

\(a|b\wedge a|(b+c)\Rightarrow \exists r,s \in \mathbb{Z}\) mit

\(b=ra\) und \(b+c=sa\), also

\(c=sa-ra=(s-r)a\), d.h. \(a|c\), Widerspruch zu \(a\not | \,c\).