Hallo Sophie,
Franz ist 1 Jahr alt, Walter ist 11 und Waltraud ist 15 Jahre alt.
Denke Dir die drei Alter als Säulen von Jahren - so wie hier
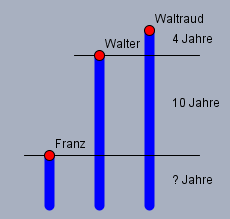
Die Summe aller drei Säulen ist 27. Das Stück von Waltraud, das über Walter hinaus ragt, sind 4 und die beiden Stücke zwischen Franz und Walter sind \(2 \cdot 10 =20\) Jahre. Wenn man nun von der Summe \(27\) die bekannten Stücke abzieht$$27 - 4 - 20 = 3$$bleiben 3 Jahre über, die sich auf drei Säulen aufteilen. D.h. pro Säule ist es nur 1 Jahr.
Folglich ist Franz nur ein Jahr alt, usw.
Gruß Werner