Verhältnis des Radius des Kreises K zum Radius des Halbkreises Hk?

Question

Ein Quadrat mit zwei angesetzten Halbkreisen Hk bildet eine Herzform, die wiederum von einem Kreis K eingeschlossen wird. In welchem Verhältnis steht der Radius des Kreises K zum Radius des Halbkreises Hk?

Answer 1

Hm,

ich hab das ähnlich angegangen wie abakus

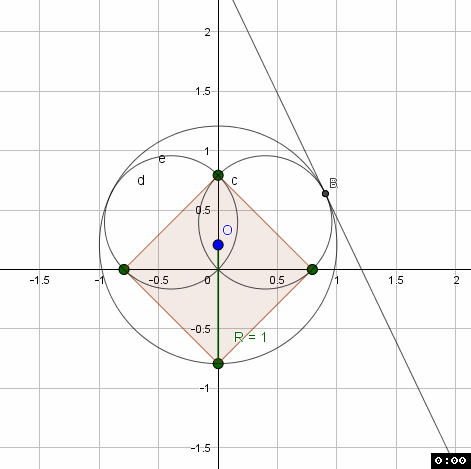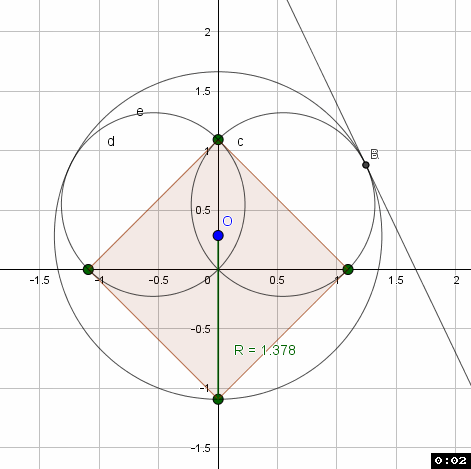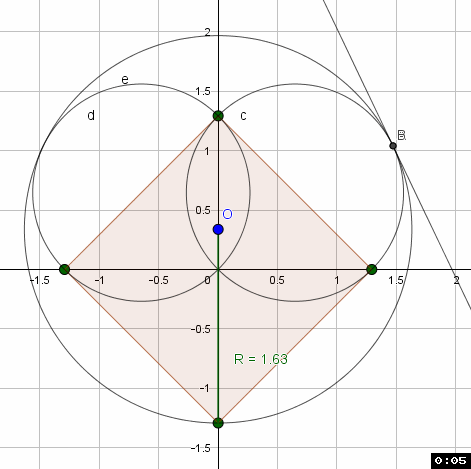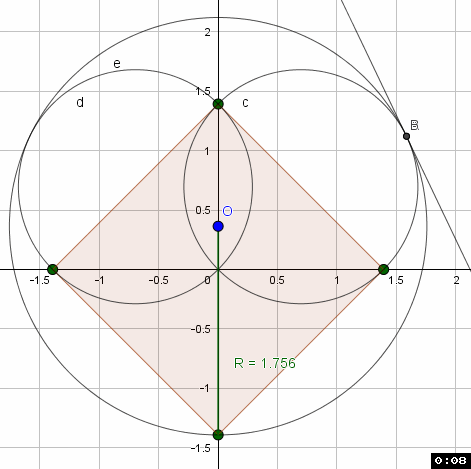
Quadrat_a={(0, -1), (1, 0), (0, 1), (-1, 0)}

K_R:(0,o)+ (o+a) (cos(t),sin(t))

k_r:(( (a) / 2, (a) / 2))+ a sqrt(2)/2 (cos(t),sin(t))

K_R = k_r

---- hässliche Rechnung (bekommt man vielleicht schöner hin, aber erstmal ein Ansatz)

\( R \, :=  \, a + \frac{1}{2} \cdot \frac{a \; \left(\sqrt{2} - 2 \right) \; \operatorname{cos} \left( 2 \; \operatorname{tan⁻^1} \left( \frac{1}{7} \; \left(\sqrt{2} - 3 \right) \right) \right) + a}{\operatorname{cos} \left( 2 \; \operatorname{tan⁻^1} \left( \frac{1}{7} \; \left(\sqrt{2} - 3 \right) \right) \right)} \)

\(r \, :=  \, a \; \frac{\sqrt{2}}{2}\)

\(r/R=\sqrt{2} \cdot \frac{\operatorname{cos} \left( 2 \; \operatorname{tan⁻^1} \left( \frac{1}{7} \; \left(\sqrt{2} - 3 \right) \right) \right)}{\sqrt{2} \; \operatorname{cos} \left( 2 \; \operatorname{tan⁻^1} \left( \frac{1}{7} \; \left(\sqrt{2} - 3 \right) \right) \right) + 1}=0.56066\)

Comments

Hässliche Rechnung (bekommt man vielleicht schöner hin).

---

Yep :-),

Schöngerechnet mit a aus meinem KO komm ich dann auf

\( \left\{ o = \frac{2 \; \sqrt{2} - 1}{7} \; a, R=\frac{a}{7} \left(2 \; \sqrt{2} + 6 \right) ,\; r =  \frac{1}{2} \; \sqrt{2} \; a,\; \frac{r}{R}=\frac{1}{4} \; \left(3 \; \sqrt{2} - 2 \right) \right\} \)

Answer 2

Ich lege mal ein KoSy rein (waagerechte grüne Linie als Abszissenachse, Halbdiagonale des Quadrats als eine Längeneinheit). Warum sich dann oben rechts das abgebildete grüne Quadrat ergibt, mögen Interessierte selbst herausfinden.

Der Radius (blau) ist dann einerseits 1+a, andererseits \( \sqrt{1^2+(1-a)^2} \).

Gleichsetzen beider Radien und quadrieren:

\(1+2a+a^2=1^2+1^2-2a+a^2\), was sich zu 4a=1 bzw. a=0,25 vereinfachen lässt.

Der Radius des großen Kreises ist somit 1,25, der Radius des Halbkreises ist 0,5\( \sqrt{2} \).

Das Verhältnis der Radien ist somit 5 : (2\( \sqrt{2}\)).

Comments

Vielen Dank für deinen Lösungsversuch. Konntest du dein Ergebnis zeichnerisch erhärten? Ich nicht.

---

Du hast recht, es passt nicht.

---

Neuer Versuch: Der Kreis um (0|a) mit dem Radius 1+a hat die Gleichung
x²+(y-a)²=(1+a)².
Er soll den Kreis mit dem Mittelpunkt (0,5|0,5) und dem Radius \(0,5\sqrt{2}\) berühren.
Dieser hat die Gleichung (x-0,5)²+(y-0,5)²=0,5.
a muss dann so gewählt werden, dass das System der beiden Gleichungen genau eine Lösung hat.

---

Vielleicht besser mit dem Kosinussatz?