 Aufgabe:
Aufgabe:
Gegeben ist die Seitenlänge a für das Quadrat. Bestimmen Sie den Radius des Kreises in Abhängigkeit von a.
Problem/Ansatz:
Mein Ansatz steht soweit und ich habe auch ein Ergebnis:
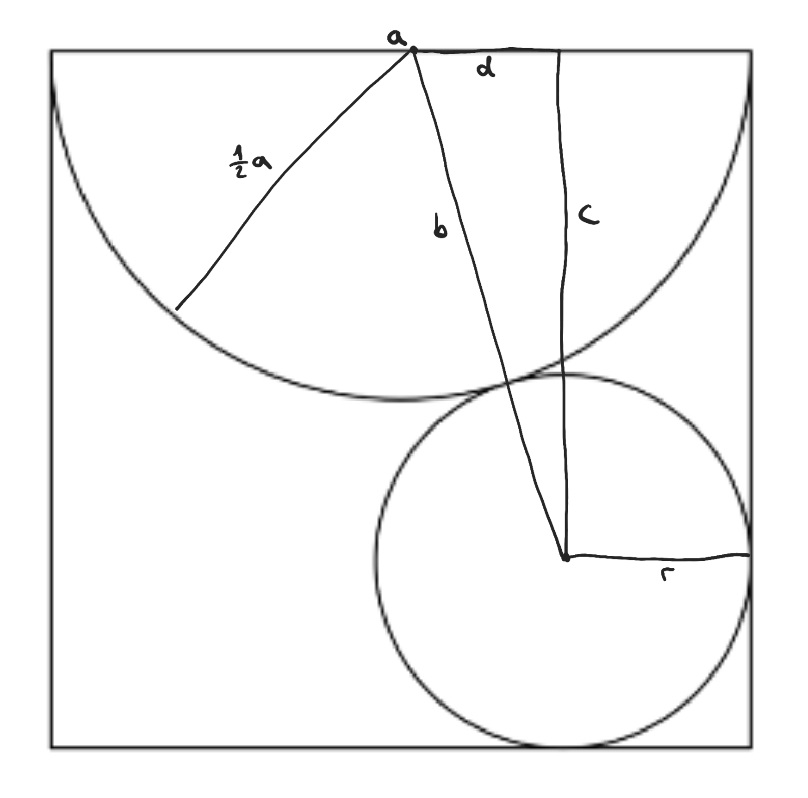
Ich stelle ein rechtwinkliges Dreieck wie im Bild zu sehen auf, um den Satz des Pythagoras anwenden zu können.
b = \( \frac{1}{2} \)a + r
c = a - r
d = \( \frac{1}{2} \)a - r
mit \( b^{2} \) = \( c^{2} \) + \( d^{2} \)
Dann ist ( \( \frac{1}{2} \)a - r)2 + \( (a-r)^{2} \) = \( ((\frac{1}{2})a + r)^{2} \)
Binomische Formeln aufgelöst:
\( \frac{1}{4} \) \( a^{2} \) - ar + \( r^{2} \) + \( a^{2} \) - 2ar + \( r^{2} \) = \( \frac{1}{4} \) \( a^{2} \) + ar + \( r^{2} \)
\( r^{2} \) - 3ar + \( a^{2} \) = ar
\( r^{2} \) - 4ar = - \( (a)^{2} \)
Nach quadratischer Ergänzung:
\( r^{2} \) - 4ar + \( (2a)^{2} \) = - \( (a)^{2} \) + \( (2a)^{2} \)
\( (r-2a)^{2} \) = 3\( a^{2} \)
Wurzel ziehen:
r1/2 - 2a = ± \( \sqrt{3* a^{2}} \)
r1 = 2a + a * \( \sqrt{3} \) = (2+\( \sqrt{3} \)) * a
r2 = 2a - a * \( \sqrt{3} \) = (2-\( \sqrt{3} \)) * a
Eigentlich müsste ich doch nur einen Radius erhalten, oder? Ansonsten stellt sich mir die Frage, wie der Radius, abhängig von a, sowohl r1 als auch r2 sein kann, also 2 verschiedene Größen (gleichzeitig) annehmen kann.