Zeigen Sie, dass der Flächeninhalt des Parallelogramms AA‘‘B‘‘B gleich der Summe der Flächeninhalte der …

Question

Aufgabe:

Gegeben sei ein Dreieck ABC mit zwei auf den Seiten AC und BC (nach außen hin) errichteten Parallelogrammen ACC‘A‘ und BB‘C‘‘C‘. Sei S der Schnittpunkt der Geraden A‘C‘ und B‘C‘‘. Seien A‘‘ und B‘‘ die Punkte, sodass  AA‘‘ und BB‘‘ jeweils parallel zu SC und gleich lang wie SC sind und AA‘‘B‘‘B ein (nach außen hin) errichtetes Parallelogramm auf der Seite AB des Dreiecks ergibt.

Zeigen Sie, dass der Flächeninhalt des Parallelogramms AA‘‘B‘‘B gleich der Summe der Flächeninhalte der Parallelogramme ACC‘A‘ und BB‘C‘‘C ist.

Answer 1

Hallo,

die Hauptarbeit bei dieser Aufgabe besteht wohl darin, aus der Aufgabenbeschreibung folgende Skizze anzufertigen. Wobei ...

.... auf den Seiten AC und BC (nach außen hin) errichteten Parallelogrammen ACC‘A‘ und BB‘C‘‘C‘.

... das zweite Parallelgramm wohl \(BB'C''C\) sein soll, also mit dem Punkt \(C\) als 4. Punkt!

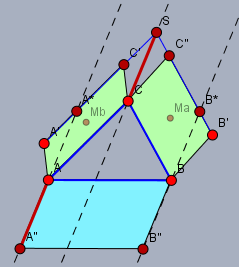
Durch zweimaliges Scheren lassen sich die beiden grünen Parallelogramme in das jeweilige Teilparallelogramm des blauen Parallelogramms überführen. 1. Scherung des linken Parallelogramm von \(A'C'\) nach \(A^*S\) und 2. Scherung von \(SC\) auf die Seite \(c\), so dass der gescherte Punkt \(C\) auf \(c\) zu liegen kommt. Und da gleiche nochmal auf der rechten Seite.

Falls Du es nicht sofort siehst, so melde Dich bitte nochmal.

Gruß Werner