Aufgabe:
Klammern auflösen partielle Ableitungen
Problem/Ansatz:
Ich versuche diese Rechnung hier nachzuvollziehen, aber kriege es nicht hin, die Rechnung richtig auszuführen. Habe es bereits mit normalem ausmultiplizieren und Produktregel versucht, aber komme nicht auf das richtige Ergebnis...
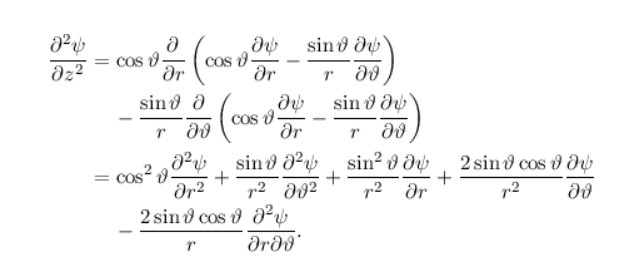
Text erkannt:
\( \begin{aligned} \frac{\partial^{2} \psi}{\partial z^{2}}=& \cos \vartheta \frac{\partial}{\partial r}\left(\cos \vartheta \frac{\partial \psi}{\partial r}-\frac{\sin \vartheta}{r} \frac{\partial \psi}{\partial \vartheta}\right) \\ &-\frac{\sin \vartheta}{r} \frac{\partial}{\partial \vartheta}\left(\cos \vartheta \frac{\partial \psi}{\partial r}-\frac{\sin \vartheta}{r} \frac{\partial \psi}{\partial \vartheta}\right) \\=& \cos ^{2} \vartheta \frac{\partial^{2} \psi}{\partial r^{2}}+\frac{\sin \vartheta}{r^{2}} \frac{\partial^{2} \psi}{\partial \vartheta^{2}}+\frac{\sin ^{2} \vartheta}{r^{2}} \frac{\partial \psi}{\partial r}+\frac{2 \sin \vartheta \cos \vartheta}{r^{2}} \frac{\partial \psi}{\partial \vartheta} \\ &-\frac{2 \sin \vartheta \cos \vartheta}{r} \frac{\partial^{2} \psi}{\partial r \partial \vartheta} . \end{aligned} \)
Ich komme nur auf das hier...
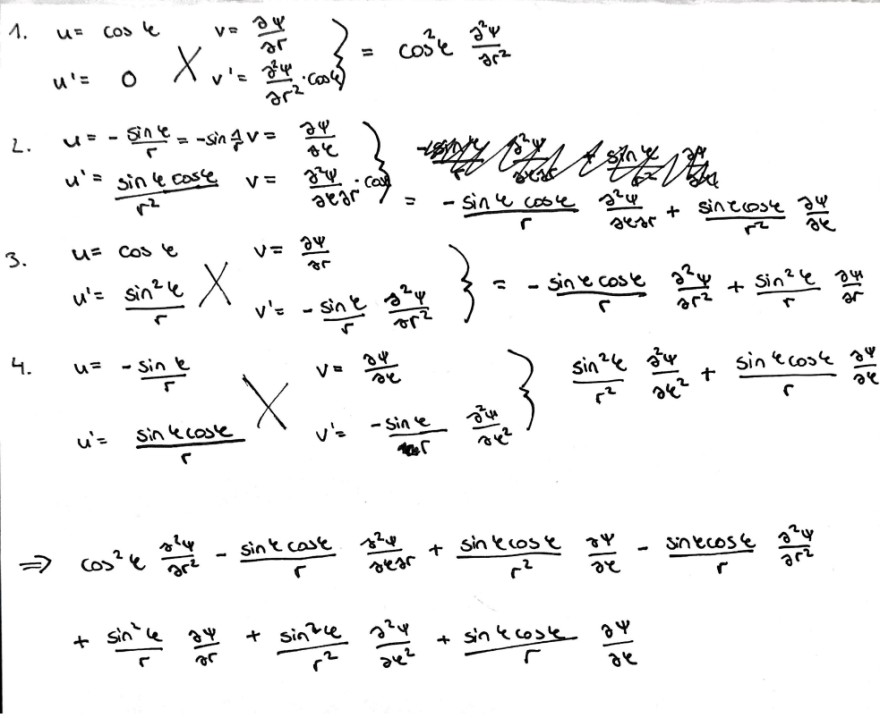
Text erkannt:
3. \( u=\cos \varphi \quad v=\frac{\partial \psi}{\partial r} \quad \frac{-\sin \varphi \cos \varphi}{r} \frac{\partial^{2} \psi}{\partial r e r}+\frac{\sin e \cos \varphi}{r^{2}} \frac{\partial \psi}{\partial r} \)
\( \left.u^{\prime}=\frac{\sin ^{2} \varphi}{r} X \quad \begin{array}{l}v=\frac{\partial \psi}{\partial r} \\ v^{\prime}=-\frac{\sin \varphi}{r} \frac{\partial^{2} \psi}{\sigma r^{2}}\end{array}\right\}=-\frac{\sin \varphi \cos \varphi}{r} \frac{\partial^{2} \psi}{\partial r^{2}}+\frac{\sin ^{2} \varphi}{r} \frac{\partial \psi}{\partial r} \)
4. \( \begin{aligned} u &=-\frac{\sin \psi}{r} \\ u &=\frac{\sin \varphi \cos \varphi}{r} \end{aligned} \quad \begin{array}{l}v=\frac{\partial \psi}{\partial r} \\ v^{\prime}\end{array} \)
\( \Rightarrow \cos ^{2} \varphi \frac{r^{2} \psi}{\partial r^{2}}-\frac{\sin \varphi \cos \varphi}{r} \frac{\partial^{2} \psi}{\partial \varphi \partial r}+\frac{\sin \varphi \cos \varphi}{r^{2}} \frac{\partial \psi}{\partial \varphi}-\frac{\sin \varphi \cos \varphi}{r} \frac{\partial^{2} \psi}{\partial r^{2}} \)
\( +\frac{\sin ^{2} \varphi}{r} \frac{\partial \psi}{\partial r}+\frac{\sin ^{2} \varphi}{r^{2}} \frac{\partial^{2} \psi}{\partial \psi^{2}}+\frac{\sin \varphi \cos \varphi}{r} \frac{\partial \psi}{\partial \varphi} \)