Aufgabe: Konvergenbereich der Potenzreihe bestimmen
Problem/Ansatz: Warum geht der Grenzwert der Folge für |x|<=1 gegen null und für |x|>1 gegen unendlich ? 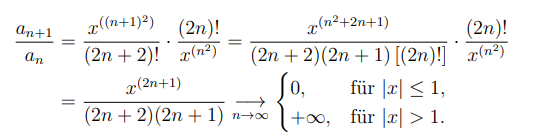
Text erkannt:
\( \begin{aligned} \frac{a_{n+1}}{a_{n}} &=\frac{x^{\left((n+1)^{2}\right)}}{(2 n+2) !} \cdot \frac{(2 n) !}{x^{\left(n^{2}\right)}}=\frac{x^{\left(n^{2}+2 n+1\right)}}{(2 n+2)(2 n+1)[(2 n) !]} \cdot \frac{(2 n) !}{x^{\left(n^{2}\right)}} \\ &=\frac{x^{(2 n+1)}}{(2 n+2)(2 n+1)} \underset{n \rightarrow \infty}{\longrightarrow}\left\{\begin{array}{ll}0, & \text { für }|x| \leq 1, \\ +\infty, & \text { für }|x|>1\end{array}\right.\end{aligned} \)