Flächenberechnung mit Gerade parallel zur x-Achse

Question

Aufgabe:

Eine Fläche wird durch

f(x) = -0,0265x² - 5,3x + 0,5

h(x) = -3,55•10^-6•x³ + 0,004x² - 1,62x + 265,5

y = 150

y = 265,5

vollständig begrenzt.

Gesucht ist der Inhalt dieser Fläche.

Problem/Ansatz:

Wie ich das mit dem Integral etc alles machen müsste, ist mir zwar klar, schwierigkeiten bereitet mir lediglich die y=150 als gerade parallel zur xAchse da ja nur die Fläche DARÜBER berechnet werden soll. ich bin mir sicher dass es dafür eine einfache 'formel' gibt, welche ich aber grad absolut nicht finde. irgendwie vor dem gesamten integral was mit n - integal?? wer kann helfen?

Answer 1

Näherungsweise setzt sich die Fläche aus 3 Integralen zusammen

∫ (-100 bis -33.98) (265.5 - (- 0.0265·x² - 5.3·x + 0.5)) dx
+ ∫ (-33.98 bis 0) (265.5 - 150) dx
+ ∫ (0 bis 89.51) ((- 3.55·10^(-6)·x³ + 0.004·x² - 1.62·x + 265.5) - 150) dx = 11214

Ich denke du kannst hier auch sehen wie man die Integrale aufstellt. Im Grunde berechnet man immer nur die Fläche zwischen 2 Funktionen.

Comments

Das hilft mir sehr weiter, vielen dank.

nur eine frage noch, wie entsteht die -100 als untere Grenze beim ersten Intervall? wenn ich mir den Schnittpunkt von -0,0265x²-5,3x+0,5 und y=150 anzeigen lasse, komme ich da auf -166,02 ?

---

nur eine frage noch, wie entsteht die -100 als untere Grenze beim ersten Intervall

- 0.0265·x² - 5.3·x + 0.5 = 265.5

Schau dir auch eine Skizze an

Plotlux öffnen

f₁(x) = -0,0265x²-5,3x+0,5f₂(x) = -3,55·10^(-6)·x³+0,004x²-1,62x+265,5f₃(x) = 150f₄(x) = 265,5Zoom: x(-110…100) y(140…270)

Answer 2

Hallo

hast du dir die Dinger plotten lassen?

du brauchst die Schnittpunkte der 2 Polynomen mit den Geraden, dann hast du 3 Bereiche; f über der unteren Geraden also f-150  nur die 2 Geraden also 265,5 -150 ein Rechteck , h zwischen den 2 Geraden also h-150  die 3 Integrale ausrechnen,

Gruß lul

Answer 3

Hilft das weiter?                                                                                      .

Comments

Für den exakten Wert des Flächeninhalts, bestehend aus drei Teilflächen wie von Lul beschrieben, komme ich auf eine ziemlich unhandliche Formel. Gerundet komme ich auf 11214.

Answer 4

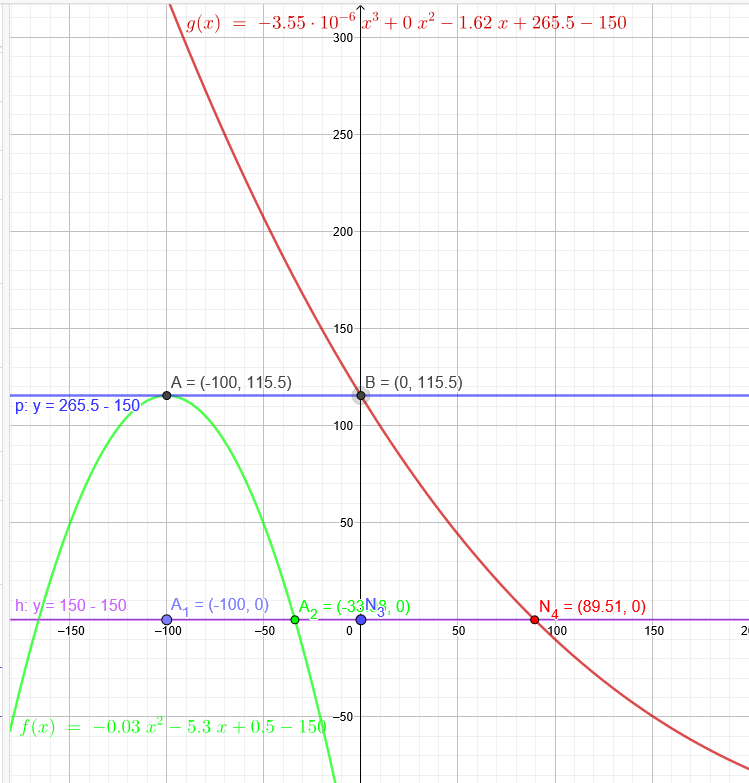
Ich verschiebe alle Graphen um 150 L E nach unten, damit die Abgrenzungen deutlicher zu sehen sind:

1.Fläche:

Rechteck A₁, N₃, B und A: $100*115,5=11550FE$

2.Fläche unter der grünen  Parabel:  $\int\limits_{-100}^{-33,98}(-0,03x^2-5,3x-149,5)*dx$

Zu berechnende Fläche in dem Bereich:

$-100≤x≤0 → 11550FE-\int\limits_{-100}^{-33,98}(-0,03x^2-5,3x-149,5)*dx$

3.Fläche unter der roten kubischen Parabel: $0≤x≤89,51$  →

$\int\limits_{0}^{89,51}(-3,55* 10^{-6}x^3+0,004x^2-1,62x+115,5)*dx$

$A= 11550FE-\int\limits_{-100}^{-33,98}(-0,03x^2-5,3x-149,5)*dx$+

$\int\limits_{0}^{89,51}(-3,55* 10^{-6}x^3+0,004x^2-1,62x+115,5)*dx$