Aufgabe:
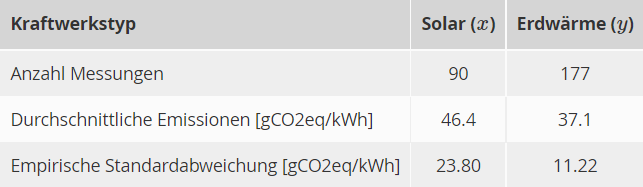
Für Solar-Kraftwerke und Erdwärme-Kraftwerke liegen Ihnen verschiedene statistische Kennwerte von deren Emissionen während des gesamten Lebenszyklus der Kraftwerke vor. Die unterschiedlichen Emissionen sind in CO2-Äquivalente ausgedrückt und werden in Gramm pro Kilowattstunde angegeben [gCO2eq/kWh]. Die durchschnittlichen Emissionen pro Kraftwerkstyp und die entsprechende empirische Standardabweichung sowie die Zahl der Messungen sind in der folgenden Tabelle zusammengefasst.
Text erkannt:
\begin{tabular}{|l|c|c|}
\hline Kraftwerkstyp & Solar \( (x) \) & Erdwärme \( (y) \) \\
\hline Anzahl Messungen & 90 & 177 \\
\hline Durchschnittliche Emissionen [gCo2eq/kWh] & \( 46.4 \) & \( 37.1 \) \\
\hline Empirische Standardabweichung [gCo2eq/kWh] & \( 23.80 \) & \( 11.22 \) \\
\hline
\end{tabular}
Können Sie statistisch nachweisen, dass die durchschnittliche Höhe der Emissionen von Erdwärme-Kraftwerken signifikant verschieden sind von jener von Solar-Kraftwerken? (Alternativhypothese). Beantworten Sie diese Frage mittels eines Tests auf Erwartungswerte und gehen Sie von Varianzgleichheit aus (Signifikanzniveau 10%).
a. Wie lautet der Absolutbetrag der Teststatistik?
4.34
b. Wie lautet der Absolutbetrag des kritischen Wertes? (Runden Sie das Ergebnis auf 4 Nachkommastellen.)
1.6506
Problem/Ansatz:
die a ist richtig
kann mir jemand bei der b bitte weiterhlefen?
Dieses Ergebnis ist nämlich falsch
Mit R:
n <- 90
mean_stamm <- 46.4
sd_stamm <- 23.80
n_andere <- 177
mean_andere <- 37.1
sd_andere <- 11.22
# b) Wie lautet der Absolutbetrag des kritischen Wertes?
df <- (90-1) + (177-1)
t_krit <- qt(0.10/2,df)