Gleichung einer Parabel 3. Grades durch Ursprung bestimmen. Hochpunkt P(5/6.25)

Question

Eine Parabel 3ten Grades geht durch den Ursprung und hat den Hochpunkt P(5/6,25).

Geht es dass ich f'(0) =0 setze?

Ich muss die Parabelgleichung ausrechnen

Answer 1

Nein, das geht nicht. Deine Informationen sind die folgenden:

f(5) = 6,25

f'(5) = 0

f(0) = 0

(f''(5) < 0)

 

Damit lässt sich nun ein Gleichungssystem für die Parameter der Funktion aufstellen.
Eine allgemeine Funktion dritten Grades hat die Gleichung:

f(x) = ax³+bx²+cx+d
f'(x) = 3ax² + 2bx + c
f''(x) = 6ax + 2b

Du erhältst die Gleichungen:

0 = d

6,25 = a*125 + b*25 + c*5

0 = 3a*25 + 2b*5 + c

 

Das reicht aber nicht aus, um alle Variablen zu bestimmen, dafür benötigst du eine weitere Information. Möglicherweise steht noch etwas in der Aufgabe, was a=1 suggeriert?
 

Dann ließe sich das System lösen:
6,25 = 125 + b*25 + c*5

0 = 75 + 10b + c

Zieht man fünf mal die zweite von der ersten Gleichung ab, erhält man:

6,25 = 125-5*75 + 25b - 50b

25 b = 125-5*75 - 6,25

b = -10,25

⇒ c = -75 - 10*b = 27,5

 

Die Lösung wäre also

f(x) = x³ - 10,25 x² + 27,5 x

Answer 2

f ' (0) = 0 kannst du nicht einfach annehmen.

 

Die Bedingungen aus dem Hochpunkt:

f '(5) = 0

f(5) = 6.25

und

Ursprung auf dieser Parabel heisst:

f (0) = 0

Answer 3

Was meinst Du mit einer Parabel dritten Gerades ? Du hast hier drei Bedingungen:

f(0) = 0
f(5) = 6,25
f '(5) = 0

Da langt eine ganz normale Parabel. Am besten stellt man hier direkt die Scheitelpunktform auf, weil man den Scheitelpunkt ja kennt.

f(x) = a * (x - Sx)^2 + Sy = a * (x - 5)^2 + 6,25

a ist der Öffnungsfaktor. Der lässt sich aus dem Scheitelpunkt und einem weiteren Punkt der Parabel sehr leicht bestimmen über

a = (Py - Sy) / (Px - Sx)^2 = (0 - 6,25) / (0 - 5)^2 = -6,25 / 25 = -1/4

Die Parabel in der Scheitelpunktform lautet also

 

f(x) = -1/4 * (x - 5)^2 + 6,25

Hier noch eine Zeichnung:

 

Comments

Wenn einem ganz viel dran liegt, kann man die Scheitelpunkt-Form noch ausmultiplizieren und erhält die allgemeine Form.

f(x) = -1/4 * (x - 5)^2 + 6,25
f(x) = -1/4 * (x^2 - 10x + 25) + 6,25
f(x) = -1/4 x^2 + 5/2 x

Ich bin aber der Meinung das es nicht not tut, wenn es nicht in der Aufgabe gefordert ist.

Fazit: Der faule Mathematiker tut nichts, was nicht ausdrücklich gefordert ist :)

Wenn man tatsächlich eine ganz rationale Funktion 3. Gerades haben möchte, dann bräuchte man noch eine weitere Bedingung.

Answer 4

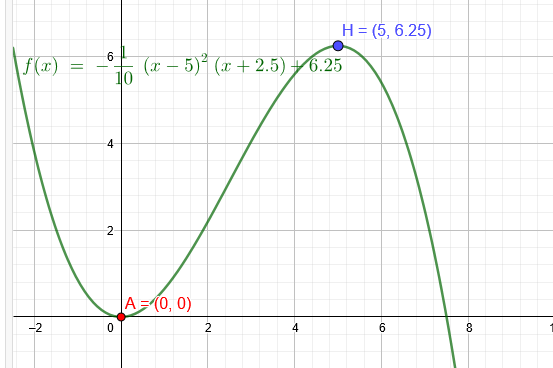
"Eine Parabel 3.ten Grades geht durch den Ursprung A(0|0) und hat den Hochpunkt P(5|6,25)."

Lösung über die Nullstellenform der kubischen Parabel:

Ich verschiebe den Graph um 6,25 Einheiten nach unten: Hochpunkt P´(5|0)  doppelte Nullstelle und            A´(0|-6,25)  

f(x)=a*(x-5)^2*(x-N)

A´(0|-6,25) 

f(0)=a*(0-5)^2*(0-N)=-25a*(N)

1.)-25a*N=-6,25 → 25a*N=6,25   → a=\( \frac{1}{4N} \)

Extremwerteigenschaft des Hochpunktes:

f´(x)=\( \frac{1}{4N} \)*[2*(x-5)*(x-N)+(x-5)^2]

f´(0)=\( \frac{1}{4N} \)*[2*(0-5)*(0-N)+(0-5)^2]

2.) \( \frac{1}{4N} \)*[2*(0-5)*(0-N)+(0-5)^2]=0  → 10N+25=0  → N=- 2,5        a=-\( \frac{1}{10} \)

f(x)=-\( \frac{1}{10} \)*(x-5)^2*(x+2,5)

Nun wieder 6,25 Einheiten nach oben:

p(x)=-\( \frac{1}{10} \)*(x-5)^2*(x+2,5)+6,25