Punkt an einer Ebene spiegeln

Question

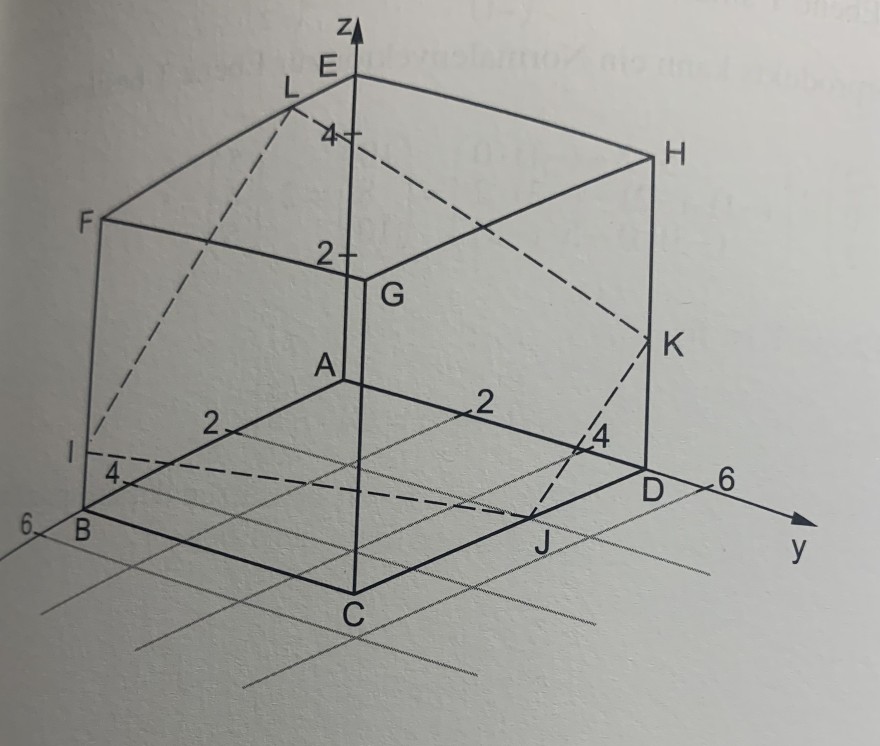
Wir haben die Ebene T mit den Eckpunkten I(5/0/1), J(2/5/0), K(0/5/2) und L(1/0/5).

Diese Ergeben die Ebene T: 5x + 4y + 5z = 30

Aufgabe:

Spiegelt man T an der Ebene mit der Gleichung x = 2,5, so erhält man die Ebene T‘.

Zeigen Sie, dass T‘ durch die Gleichung -5x + 4y + 5z = 5 beschrieben wird.

Frage:

Wie Spiegel ich nun T and der Ebene mit x = 2,5 und wie zeige ich, dass T‘ durch die Gleichung -5x + 4y + 5z = 5 beschrieben wird?

Comments

Hat jemand eine Idee?

Answer 1

Wie spiegelst du grundsätzlich einen x wert an der Stelle 2.5

xneu = 2.5 - (x - 2.5) = 5 - x

Also z.B.

die x Koordinate x = 4 wird dann zur x-Koordinate 1

weil 4 - 2.5 = 2.5 - 1

Ersetze also in der Gleichung einfach x durch 5 - x

5·x + 4·y + 5·z = 30
5·(5 - x) + 4·y + 5·z = 30
25 - 5·x + 4·y + 5·z = 30
- 5·x + 4·y + 5·z = 5

Das ist jetzt also deine neue Gleichung.

Comments

Die Formel lautet also für x=2,5

xneu = 2.5 - (x - 2.5) = 5 - x

Wäre dann für x=5

xneu = 5 - (x - 5) = 10 - x?

---

Genau. Das sollte so stimmen.

---

Vielen Dank! :)

---

weil's so schön ist, anbei das ganze in Geoknecht3D

(klick auf das Bild!)