Aufgabe:
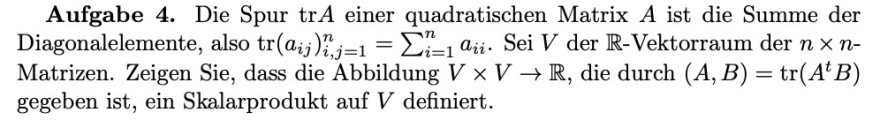
Text erkannt:
Aufgabe 4. Die Spur \( \operatorname{tr} A \) einer quadratischen Matrix \( A \) ist die Summe der Diagonalelemente, also \( \operatorname{tr}\left(a_{i j}\right)_{i, j=1}^{n}=\sum \limits_{i=1}^{n} a_{i i} \). Sei \( V \) der \( \mathbb{R} \)-Vektorraum der \( n \times n \) Matrizen. Zeigen Sie, dass die Abbildung \( V \times V \rightarrow \mathbb{R} \), die durch \( (A, B)=\operatorname{tr}\left(A^{t} B\right) \) gegeben ist, ein Skalarprodukt auf \( V \) definiert.
Problem/Ansatz:
Leider verstehe ich nicht wie das zu lösen ist. Kann mir jemand Zeigen wie das zu lösen ist?