Aufgabe:
Ein Basketballspieler erhält zwei Freiwürfe. Aus langer Beobachtung weiß er, dass er mit \( 65 \% \) Wahrscheinlichkeit beim ersten Wurf trifft. Die gleiche Trefferquote gilt auch für den zweiten Wurf. Die Wahrscheinlichkeit für zwei Treffer unmittelbar hintereinander liegt bei \( 40.95 \% \).
Wie groß ist die Wahrscheinlichkeit, dass der Spieler beim zweiten Wurf nicht trifft, wenn er beim ersten Wurf getroffen hat? (Geben Sie das Ergebnis in Prozent an.)
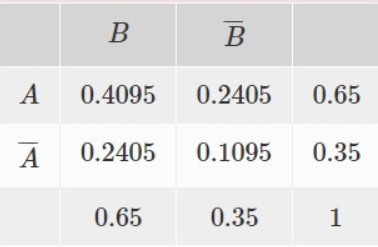
Bezeichne \( A \) das Ereignis Treffer im ersten Wurf und \( B \) das Ereignis Treffer im zweiten Wurf. Dann ist \( P(A)=P(B)=0.65 \) und \( P(A \cap B)=0.4095 \). Damit läßt sich die Vierfeldertafel aufstellen:
Problem/Ansatz:
Wie genau kommt man die Werte in der Vielfelder Tafel also das 0.65 und 0.35 ist ja in der Angabe bekannt aber was muss ich rechnen um die restlichen Felder raus zu bekommen was wäre der Rechenweg also wie kommt man zb. beim ersten Kästchen auf 0.4095 usw?
DANKE