Guten Tag!
Ich muss diese Aufgabe hier lösen, weiß aber leider nicht genau wie.
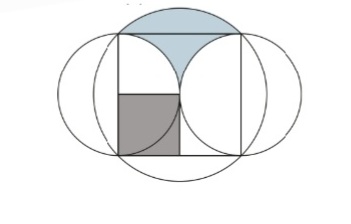
Hier bei soll ich zeigen, dass die 2 markierten Flächen den selben Inhalt haben, ohne dies jedoch konkret zu berechnen.
Alles was ich weiß ist, dass ich den erweiterten Satz des Pythagoras anwenden muss.
Wäre super, wenn mir da jemand weiterhelfen könnte!