Zeigen Sie die Behauptung für n=7 mit Hilfe von Spielsteinarithmetik.

Question

Aufgabe:

Die Summe der ersten n ungeraden Zahlen ergibt n²

Zeigen Sie die Behauptung für n=7 mit Hilfe von Spielsteinarithmetik.

Answer 1

Hallo,

Willkommen in der Mathelounge!

Mit Legosteinen dauert mir das jetzt zu lange, aber ich habe es Dir hier mal skizziert:

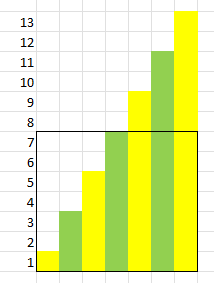
Lege die 7 Zahlen \(\{1,\,3,\,5,\,\dots \, 13\}\) so wie gezeigt mit Spielsteinen aus. Dann markiere das Quadrat \(7\times 7\) und drehe den überstehenden Teil der Steine in die Lücke innerhalb des Quadrats.

Gruß Werner

Comments

Bem.: damit ließe sich dann auch ein Beweis von \(\sum_{k=1}^n(2k-1)=n^2\) per vollständiger Induktion realisieren ;-)

Answer 2

Aloha :)

$$\begin{array}{c}\red G & \red G & \red G & \red G & \red G & \red G & \red G\\F & F & F & F & F & F & \red G\\\red E & \red E & \red E & \red E & \red E & F & \red G\\D & D & D & D & \red E & F & \red G\\\red C & \red C & \red C & D & \red E & F & \red G\\B & B & \red C & D & \red E & F & \red G\\\red A & B & \red C & D & \red E & F & \red G\end{array}$$

1 Stein mit \(\red A\)

3 Steine mit \(B\)

5 Steine mit \(\red C\)

7 Steine mit \(D\)

9 Steine mit \(\red E\)

11 Steine mit \(F \)

13 Steine mit \(\red G\)