Hallo Jan,
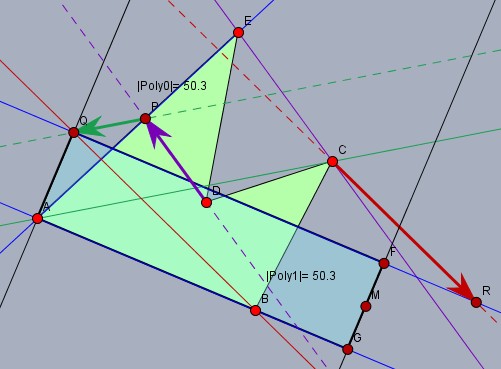
Das Fünfeck sei das Polynom \(ABCDE\). Die erste Scherung (lila) transportiert den Punkt \(D\) parallel zu \(CE\) auf die Gerade durch \(AE\). Der neue Punkt sei \(P\) und das Fünfeck wird zum Viereck \(ABCP\).
Die zweite Scherung (grün) verlegt den Punkt \(P\) parallel zu \(AC\) auf das Lot zu \(AB\) durch \(A\). Der neue Punkt sei \(Q\) und bei \(A\) entsteht ein rechter Winkel.
Für die dritte Scherung (rot) schiebt man \(C\) parallel zu \(QB\) auf die Parallele zu \(AB\) durch \(Q\). Der neue Punkt ist \(R\). Das Viereck \(ABRQ\) ist bereits ein Trapez mit einer lotrechten Seite \(AQ\).
Die letzte Scherung wird parallel zur Mittelparallelen von \(AB\) und \(QR\) ausgeführt. Der Mittelpunkt \(M\) der Strecke \(BR\) bleibt an seinem Platz und die Punkte \(B\) und \(R\) wandern nach \(G\) und \(F\). So dass \(GF\) orthogonal zu \(AB\) verläuft.
\(ABCDE\) und das Rechteck \(AGFQ\) sind flächengleich.