(Vektor) Bestimme den Abstand des Punktes M von der X-Achse

Question

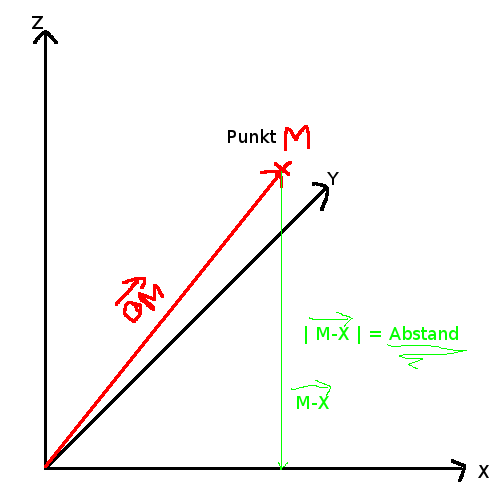
ich habe folgendes Anliegen und wäre um einen Lösungsvorschlag dankbar. Ich habe einen Punkt M=(4 5 6) im Koordinatensystem, wobei X=4, Y=5 und Z=6 und soll den Abstand des Punktes von der Z-Achse bestimmen.

Ich habe mir die Lösung so gedacht, dass ich einen Vektor 0-M habe (Ortsvektor zum Punkt M) und dann den Vektor mit dem Basisvektor Ex subtrahiere, um den Vektor M-Ex zu erhalten, wessen Betrag der Abstand zwischen dem Punkt M und der X-Achse ist.

Jedoch hänge ich irgendwie bei der Subtraktion, um den Vektor dazwischen zu erhalten, da ich nicht weiß, mit welchem Vektor ich subtrahieren soll ...

 

Skizze:

Answer 1

Du brauchst hier einfach nur den Abstand von [4,5,6] zu [4,0,0] auf der x-Achse

d = √(5^2 + 6^2) = √61

Comments

In meinen Fall wäre dann der Punkt X = (4, 0, 0)

Wenn ich den Vektor O-M von dem Vektor O-X subtrahiere, erhalte ich mit dem Betrag des Differenzvektors den Abstand √61