Unter welchem Winkel sieht man den Kreis k: (x+2)^2+(y-2)^2=20 vom Punkt Q = (3/2) aus?

Question

Aufgabe:

Unter welchem Winkel sieht man den Kreis k: (x+2)^2+(y-2)^2=20 vom Punkt Q = (3/2) aus?

Answer 1

Ich denke das ist evtl. wie folgt gemeint

Comments

SIN(α°/2) = √20/5 --> α = 126.869898°

Answer 2

Der Kreis hat den Mittelpunkt (x,y) = (-2,+2)

Die beiden Punkte (+3,+2) und (-2,+2) liegen auf der Geraden y=2.

Falls der Winkel zur x-Achse gemeint ist, beträgt der Winkel somit 0 Grad.

Comments

Vielen Dank!

Aufgrund der Angabe denke ich, dass es sich um den Winkel handelt, der sich unterhalb des Punkte Q zum Kreis hin öffnet.

Answer 3

Unter welchem Winkel sieht man den Kreis k: (x+2)^2+(y-2)^2=20 vom Punkt Q = (3|2) aus?

Ich verschiebe beide Punkte um 2 Einheiten nach unten und um 2 Einheiten nach rechts:

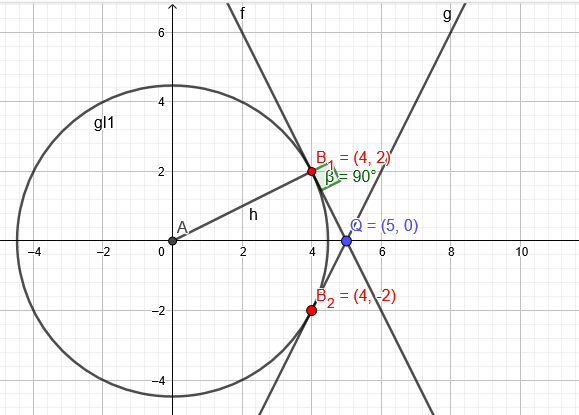
\(k´:  x^2+y^2=20→y^2=20-x^2 \)      \(Q (3|2)→ Q´(5|0)\)

Thaleskreis um \(P(2,5|0)\)     mit   \(r=2,5\)

\((x-2,5)^2+y^2=6,25\)

\((x-2,5)^2+20-x^2 =6,25→x=4→y₁=2   y₂=-2\)

Steigung der Tangente:

\(tan(α)= \frac{2-0}{4-5}=-2 \)

\(tan^{-1}(-2)= -63,43° \)

Man sieht den Kreis unter einem Winkel von \(2*63,43°=126,86°\)

Comments

Vielen Dank!