Aufgabe:
Text erkannt:
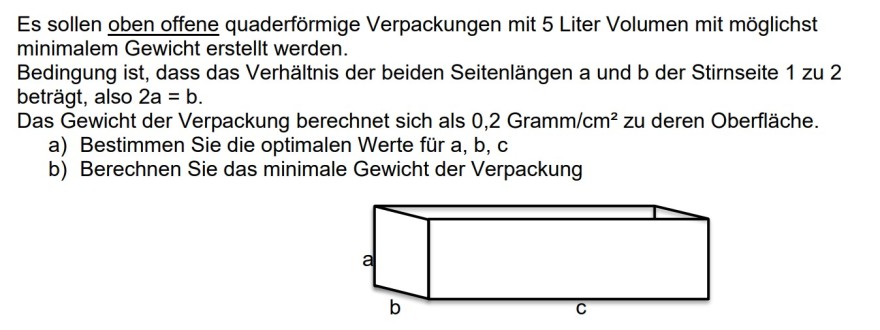
Es sollen oben offene quaderförmige Verpackungen mit 5 Liter Volumen mit möglichst minimalem Gewicht erstellt werden.
Bedingung ist, dass das Verhältnis der beiden Seitenlängen a und \( b \) der Stirnseite 1 zu 2 beträgt, also \( 2 \mathrm{a}=\mathrm{b} \).
Das Gewicht der Verpackung berechnet sich als 0,2 Gramm/ \( \mathrm{cm}^{2} \) zu deren Oberfläche.
a) Bestimmen Sie die optimalen Werte für a, b, c
b) Berechnen Sie das minimale Gewicht der Verpackung
Problem/Ansatz:
Ich versuche aktuell, die o.g. Optimierungsaufgabe zu lösen. Leider erhalte ich nach Null-setzen der ersten Ableitung ein ziemlich unrealistisches Ergebnis, weshalb ich mich erkundigen möchte, ob ich bis zum Null-setzen alles soweit richtig erfasst habe.
Aus der o.g. Aufgabenstellung habe ich folgendes extrahiert:
Gegeben
b = 2a
Hauptbedingung:
O = min
O = 2ab + 3ac = 4a^2 + 3ac (da b = 2a)
Nebenbedingung:
V = abc = 2a^2 * c (da b = 2a)
V = 5L = 5000cm^3
V umgstellt nach c:
c = 2500/a^2
Eingesetzt n O:
O = 4a^2 + 3a(2500/a^2) = min
1. Ableitung:
O' = 8x - (7500/x^2)
Wenn ich O' = 0 setze, erhalte ich ein ziemlich komplexes Ergebnis, welches ich mit einem Online-Taschenrechner lösen musste und das Dinge wie komplexe Zahlen enthält, welche wir im Unterricht bisher nicht behandelt haben. Ferner ist für die Aufgabe das minimale Gewicht (m = 278g) zur Kontrolle gegeben, was sich mit meinem bisherigen Vorgehen nicht erreichen lässt.
Hat jemand eine Idee, wo mein Verständnisfehler liegt?