Aufgabe: folgende graphische Lösung
eines linearen Optimierungsmodells ist gegeben.
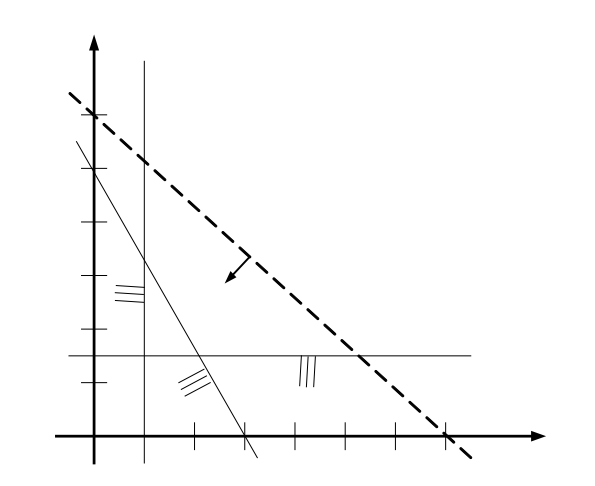
Problem/Ansatz: Geben Sie die optimalen
Variablenwerte an. Wie hoch ist der
erzielte Zielfunktionswert?
Hi, ich hätte das LP so aufgestellt:
ZF = 3*x1 + 5*x2
NB: 1,5 x2
1 x1
3*x1 + 5*x2
x1, x2 > 0
stimmt das bsiher so? und wie komme ich jetzt auf die Iso- Kosten - Linie?
LG