Hallo zusammen!
Die Aufgabe lautet:
Zwei Kugelflächen mit den Mittelpunkten M1,M2 und den Radien r1, r2 schneiden sich in einem Kreis. Es seien P ein Punkt der Schnittkreisebene E außerhalb der Kugeln sowie B1,B2 die Berührpunkte zweier Tangenten von P aus an die Kugeln. Weiter sei S der Schnittpunkt von E und M1 M2.
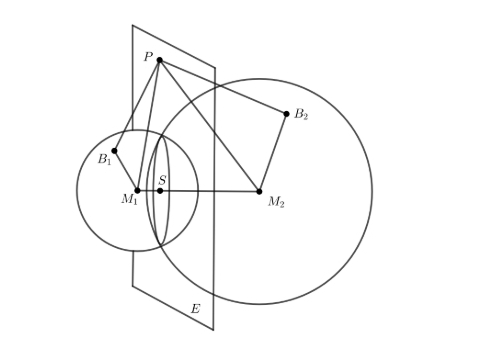
Weitergehend sei in der Folgenden Figur a1:= |M1S|, a2:= |M2S| und ρ der Radius des Schnittkreises S.
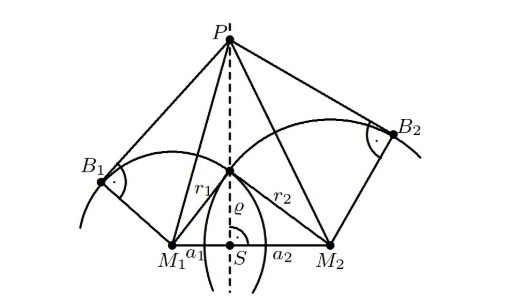
Zeigen Sie, dass \( \left|P B_{1}\right|^{2}=\left|P B_{2}\right|^{2} \) gilt, indem Sie eine gültige Gleichungskette
\( \left|P B_{1}\right|^{2}=\cdots=\left|P B_{2}\right|^{2} \)
hinschreiben, in der folgende Terme je genau einmal vorkommen:
\( |P S|^{2}+a_{1}^{2}-r_{1}^{2}, \quad|P S|^{2}+a_{2}^{2}-r_{2}^{2}, \quad\left|P M_{1}\right|^{2}-r_{1}^{2}, \quad\left|P M_{2}\right|^{2}-r_{2}^{2}, \quad|P S|^{2}-\rho^{2} \)
Begründen Sie die Gültigkeit jeder Gleichung.
Wäre super, wenn mir da jemand weiterhelfen könnte! :)
Vielen lieben Dank schon mal!