Flächeninhalt des Rechtecks soll maximal sein..?

Question

Aufgabe:

Gegeben ist die Funktion mit f(x)=1/6x^2•(6-x).
Der Punkt P(u | f(u)) mit 0 < u <6 liegt auf dem Graphen von f.

Die Koordinatenachsen und die Parallelen zu den Achsen durch P bilden ein Rechteck. Bestimmen Sie u so, dass der Flächeninhalt des Rechteckes maximal ist. Ist für diesen Wert von u der Umfang ebenfalls maximal?

Kann mir bitte wer weiterhelfen

Answer 1

Maximiere A(x)=f(x)*x indem du die Ableitung A' bildest und diese null setzt.

Answer 2

Hallo,

\( \begin{aligned} f(x) &=\frac{1}{6} x^{2} \cdot(6-x) \\ f(u) &=\frac{1}{6} u^{2} \cdot(6-u) \\ &=u^{2}-\frac{1}{6} u^{3} \end{aligned} \)

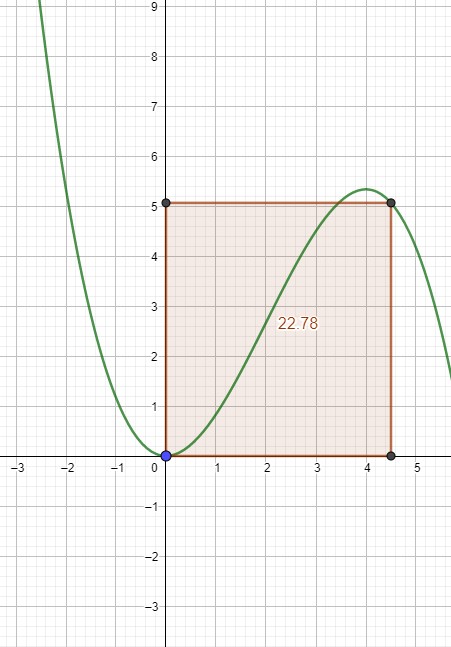
Der Flächeninhalt des Rechtecks ist u · f(u)

\( \begin{aligned} A &=u \cdot\left(u^{2}-\frac{1}{6} u^{3}\right) \\ &=u^{3}-\frac{1}{6} u^{4} \end{aligned} \)

Bilde die 1. Ableitung

\( A^{\prime}=3 u^{2}-\frac{2}{3} u^{3} \),

setzte sie = 0 und löse nach u auf.

Gruß, Silvia

Answer 3

A(u) = u·f(u) = u·(1/6·u^2·(6 - u)) = u^3 - 1/6·u^4

A'(u) = 3·u^2 - 2/3·u^3 = 0 --> u = 4.5 (∨ u = 0)

U(u) = 2·u + 2·f(u) = 2·u + 2·(1/6·u^2·(6 - u)) = - 1/3·u^3 + 2·u^2 + 2·u

U'(u) = - u^2 + 4·u + 2 = 0 --> u = 2 + √6 = 4.449

Answer 4

Hallo

hast du das gezeichnet? die eine Seite des Rechtecks ist f(u) die andere u die Fläche also A(u)= u*f(u) davon das max finden kannst du sicher ?

der Umfang ist U(u)=2u+2f(u)

Gruß lul