Funktion zu Storebelt-Brücke aufstellen

Question

Kann mir bitte jemand bei dieser aufgabe behilflich sein?

der Abstand der beiden254m hohen Pfeiler der store baelt-Brücke beträgt 1624m und wird von zwei Tragseilen überbrückt. Die Durchfahrtshöhe der Brücke beträgt 65m.

beschreiben sie die Form der Spannseile näherungsweise durch eine ganzratinale Funktion zweiten Grades. Überlegen sie zuerst eine geeignete wahl des Koordinatensystems.

ich habe wirklich keine ahnung und bin schon sehr verzweifelt :S

Answer 1

Zunächst eine Skizze:

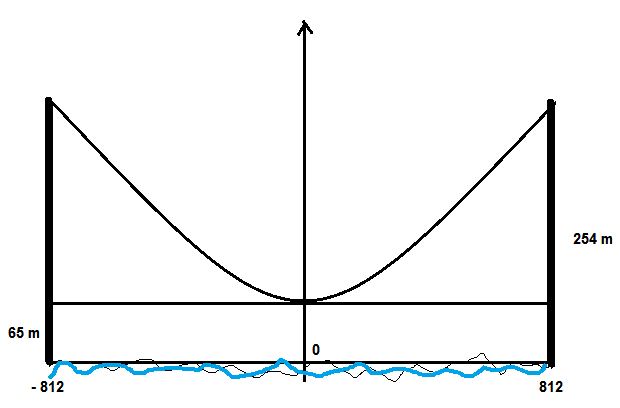
Ich habe die Brücke so ins Koordiantensystem gelegt, dass der Scheitelpunkt der Tragseilkurve in 65 Metern Höhe über dem Ursprung liegt. Der Scheitelpunkt hat dann die Koordianten S ( 0 | 65 ).

Nun die Scheitelpunktform einer quadratischen Gleichung ansetzen:

f ( x ) = a ( x - xs ) ² + ys

wobei xs, ys die x- bzw. y-Koordinaten des Scheitelpunktes sind und a der Streckfaktor, der die Form des Graphen beeinflusst.

Also Einsetzen der Koordinaten von S:

f ( x ) = a ( x - 0 ) ² + 65

<=> f ( x ) = a x ² + 65

Nun muss noch der Faktor a bestimmt werden. Dazu verwendet man die Information, dass die Spitze des rechten Pfeilers mit den Koordinaten ( 812 | 254 ) zum Graphen gehört, dass also gelten muss:

254 = a * 812 ² + 65

<=> a = ( 254 - 65 ) / 812 ²

<=> a ≈ 0,0002866

Somit lautet die gesuchte Funktion:

f ( x ) = 0,0002866 x ² + 65

Answer 2

f(x) = (254 - 65)/(1624/2)^2·x^2 + 65 = 27/94192·x^2 + 65

Skizze: