1. Ableitung von: f(x)= a*sin(pi*x+c)+d?

Question

nächste Knobelaufgabe (zumindest für mich).
Sinusfunktion f(x)= a*sin(pi*x+c)+d schneidet y-Achse in 4 und  hat im Punkt P(2/4) die Steigung m=3pi. c ist ungleich 0.
Das 1. was ich gemacht habe: P(2/4) f(2)=4 -> a*sin(pi*2+c)+d=4 -> a*sin(2pi+c)+d= 4 (weiter konnte ich es leider nicht auflösen)

Dann habe ich auch mal die 1. Ableitung probiert, bin mir aber nicht sicher, ob diese stimmt: f'(x)= a*pi*cos(pi*x+c)
Weiter weiß ich leider nicht. :-(
Wäre dankbar für jede Hilfe.
LG.

Answer 1

f(x) = a·SIN(pi·x + c) + d

f'(x) = pi·a·COS(pi·x + c)

schneidet y-Achse in 4

f(0) = 4
a·SIN(c) + d = 4

und  hat im Punkt P(2/4)

f(2) = 4
a·SIN(c) + d = 4

die Steigung m = 3pi.

f'(2) = 3·pi
pi·a·COS(c) = 3·pi

Sei c = pi

pi·a·COS(c) = 3·pi
pi·a·COS(pi) = 3·pi
a = -3

a·SIN(c) + d = 4
-3·SIN(pi) + d = 4
d = 4

Also z.B.

f(x) = - 3·SIN(pi·x + pi) + 4

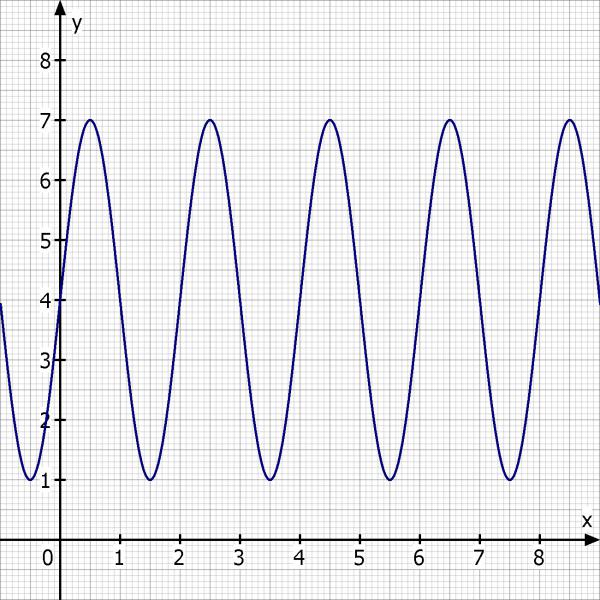
Skizze