Hallo,
a) skizziere den Graphen von f mithilfe einer Wertetabelle im Intervall [-2<x>3]
Setze die entsprechenden Werte für x ein, um die y-Koordinaten der Punkte zu erhalten. Verbinde die Punkte miteinander.
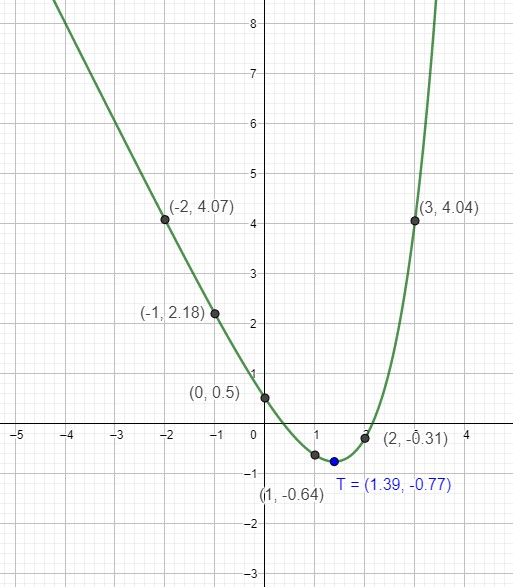
b) berechne die Lage des Minimums der Funktion f
Setze die 1. Ableitung = 0 und löse nach x auf.
Setze dein Ergebnis in die 2. Ableitung ein, um zu sehen, ob die Extremstelle ein Hoch- oder Tiefpunkt ist.
Setze dein Ergebnis in die Ausgangsfunktion ein, um die y-Koordinate des Tiefpunktes zu bestimmen.
c) zeige, dass f keine Wendepunkte besitzt
Die notwendige für Bedingung für Wendepunkte ist f''(x) = 0. Zeige, dass das hier nicht der Fall ist und melde dich, falls du noch Fragen hast.
Gruß, Silvia