Können Sie eine lineare Abbildung φ: R^4->R^2 finden, sodass Kern(φ)=H, mit
H={(x,y,z,t) aus R^4| x=y=z=t}?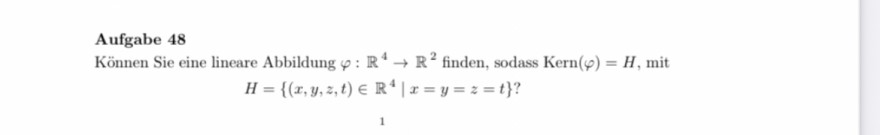
Text erkannt:
Aufgabe 48
Können Sie eine lineare Abbildung \( \varphi: \mathbb{R}^{4} \rightarrow \mathbb{R}^{2} \) finden, sodass \( \operatorname{Kern}(\varphi)=H \), mit
\( H=\left\{(x, y, z, t) \in \mathbb{R}^{4} \mid x=y=z=t\right\} ? \)
1