Gleichung einer Polynomfunktion mit bestimmten Wendepunkt erstellen

Question

Aufgabe:

Erstelle zu den gegebenen Bedingungen jeweils die zugehörige Gleichung:

Graph einer Polynomfunktion 3. Grades besitzt den Wendepunkt W(2|2), an der Stelle 3 eine Nullstelle und an der Stelle 1 ein Maximum

Problem/Ansatz:

Die Erstellung und der Aufbau einer Gleichung einer Funktion 3. Grades ist klar, nur verstehe ich nicht wie ich den Wendepunkt und die Nullstelle miteinbeziehen kann, bzw wie und wo ich diese in der Gleichung angebe? Bzw, wie ich eine Gleichung erstelle bei der ich weiss dass der WP (2|2) ist

Answer 1

Hallo

WP (2|2) liefert zwei Informationen:

f(2) = 2 und f''(2) = 0

Daraus ergeben sich die Gleichungen

8a + 4b + 2c + d = 2

12a + 4 b = 0

Nullstelle: f(3) = 0 ⇒ 27a + 9b + 3c + d = 0

Tiefpunkt bei x = 1, f'(x) = 0 ⇒ 3a + 2b + c = 0

Kommst du damit weiter?

Gruß, Silvia

Comments

Ja, Danke!! Lg

Answer 2

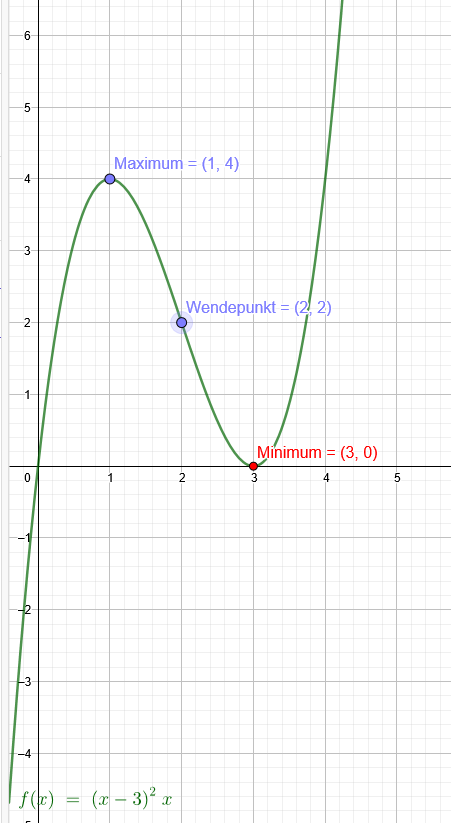
"Graph einer Polynomfunktion 3. Grades besitzt den Wendepunkt W(2|2), an der Stelle 3 eine Nullstelle und an der Stelle 1 ein Maximum

Lösung über die Nullstellenform der kubischen Parabel:

an der Stelle 3 eine Nullstelle liegt ein Minimum doppelte Nullstelle , da an der Stelle x=1 ein Maximum vorliegt  (Punktsymmetrie wegen Wendepunkt W(2|2))

\(f(x)=a*(x-3)^2*(x-N)\)

W(2|2)

\(f(2)=a*(2-3)^2*(2-N)=a*(2-N)=2→a=\frac{2}{2-N}\)

\(f(x)=\frac{2}{2-N}*[(x-3)^2*(x-N)]\)

\(f´(x)=\frac{2}{2-N}*[(2x-6)*(x-N)+(x-3)^2*1]\)

\(f´(1)=\frac{2}{2-N}*[(2-6)*(1-N)+(1-3)^2]\)

\(\frac{2}{2-N}*[(2-6)*(1-N)+(1-3)^2]=0→N=0→a=1\)

\(f(x)=(x-3)^2*x)\)