Abituraufgabe Analysis(Logik)

Question

Aufgabe:

Text erkannt:

ma723/Hle
Abituraufgabe Analysis
\( 02.06 .2022 \)
2 Luftdruck
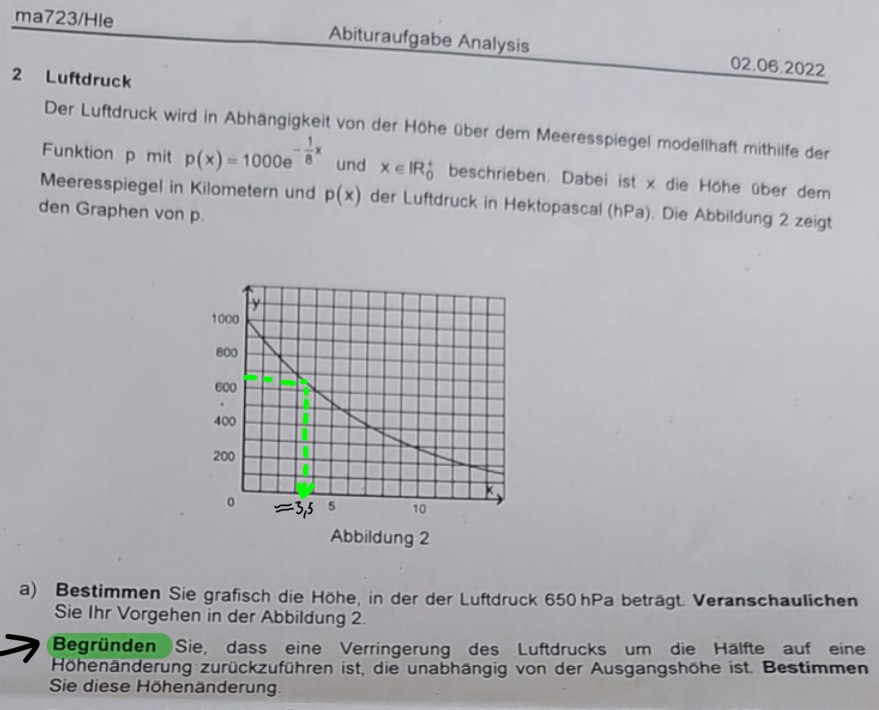
Der Luftdruck wird in Abhangigkeit von der Hohe ober dem Meeresspiegel modellhaft mithilfe der Funktion \( p \) mit \( p(x)=1000 e^{-\frac{1}{8} x} \) und \( x \in \mathbb{R}_{0}^{+} \)beschrieben. Dabei ist \( x \) die Hohe aber dem Meeresspiegel in Kilometern und \( \mathrm{p}(\mathrm{x}) \) der Luftdruck in Hektopascal (hPa). Die Abbildung 2 zeigt den Graphen von \( \mathbf{p} \).
Abbildung 2
a) Bestimmen Sie grafisch die Hohe, in der der Luftdruck \( 650 \mathrm{hPa} \) betragt. Veranschaulichen Sie Ihr Vorgehen in der Abbildung \( 2 . \)

Begründen Sie, dass eine Verringerung des Luftdrucks um die Halfte auf eine Hohenänderung zurückzuführen ist, die unabhängig von der Ausgangshöne ist. Bestimmen Sie diese Höhenänderung.

Problem/Ansatz:

Ich verstehe nicht, wie ich bei der markierten Aufgabe vorgehen sollte, um die aufgestellte Behauptung zu begründen. Wäre dankbar, falls mir da jemand weiterhelfen könnte.

Comments

Abituraufgabe Analysis(Logik)

Und was hat das mit Logik zu tun?

Answer 1

Löse die Gleichung

p(x + h) = 1/2·p(x)

Du wirst sehen, diese Gleichung ist von x unabhängig.