Aufgabe:
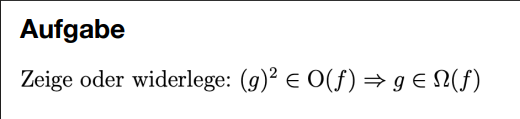
(Keine Buchseite)
Problem/Ansatz:
Ich verstehe nicht, inwiefern ich dies widerlegen soll. Mein Ansatz wäre für g(n) = n zu nehmen und für f(n) = n^2 und damit dann weiter zu gehen, da damit die erste Bedingung erfüllt ist, jedoch g als Teilmenge von Oemga von f nicht.
Soweit bin ich gekommen:
g(n) = n
f(n) = n^2;
ang. es gilt g als Teilmenge von O(f):
(Es existiert ein) c und n > 0, wobei gilt, dass c*g(n) >= f(n) ist.
nun zeigen, dass g keine Teilmenge von Omega von f ist?
Ich bitte um Hilfestellung und eventuell einer Lösung, die ich nachvollziehen kann. Es handelt sich um eine Übungsaufgabe, wobei ich die Lösung des Dozenten nicht nachvollziehen kann.