Aloha :)
1. Schritt: "Michy Maus" malen
Wir betrachten zwei Mengen \(B_1\) und \(B_2\) von Ereignissen, die kein Element gemeinsam haben, d.h. \(B_1\cap B_2=\emptyset\). Wenn wir diese beiden Mengen jeweils mit einer dritten Menge \(A\) schneiden, enhalten auch die Schnittmengen keine gemeinsamen Elemente:$$A\cap(B_1\cup B_2)=(A\cap B_1)\cup(A\cap B_2)$$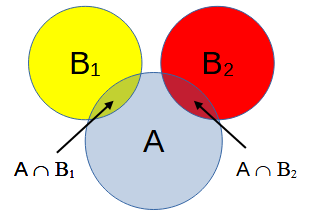
Für die Eintrittswahrscheinlichkeiten bedeutet dies:$$P(\,A\cap(B_1\cup B_2)\,)=P((A\cap B_1)\cup(A\cap B_2))=P(A\cap B_1)+P(A\cap B_2)$$
2. Schritt: Ereignis-Reihenfolge beachten
Die Wahrscheinlichkeit \(P(A\cap B)\), dass 2 Ereignisse \(A\) und \(B\) gemeinsam eintreten, kann je nach Eintritts-Reihenfolge unterschiedlich geschrieben werden:
a) \(A\) tritt vor \(B\) ein:
Die Wahrscheinlichkeit für das Eintreten von \(A\) ist \(P(A)\). Die Wahrscheinlichkeit, dass dann noch \(B\) eintritt, ist nicht \(P(B)\), sondern \(P(B|A)\), weil wir ja bereits wissen, dass \(A\) eingetreten ist:$$P(A\cap B)=P(A)\cdot P(B|A)$$
b) \(B\) tritt vor \(A\) ein:
Die Wahrscheinlichkeit für das Eintreten von \(B\) ist \(P(B)\). Die Wahrscheinlichkeit, dass dann noch \(A\) eintritt, ist nicht \(P(A)\), sondern \(P(A|B)\), weil wir ja bereits wissen, dass \(B\) eingetreten ist:$$P(A\cap B)=P(B)\cdot P(A|B)$$
3. Schritt: Die totale Wahrscheinlichkeit für \(B_1\) und \(B_2\) zusammensetzen:$$P(A\cap(B_1\cup B_2))\stackrel{(1)}{=}P(A\cap B_1)+P(A\cap B_2)\stackrel{(2b)}{=}P(B_1)P(A|B_1)+P(B_2)P(A|B_2)$$
4. Schritt: Verallgemeinern auf \(B_1,\ldots,B_n\).