Hallo
Ich muss anhand dieser Konstruktion:
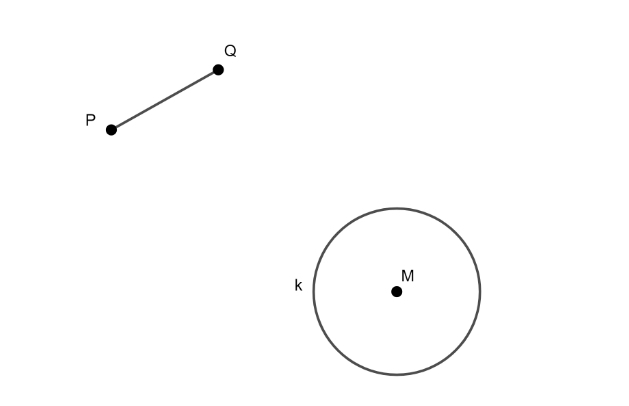
Zwei Punkte (R ∈ k und S ∈ k) konstruieren und das so, dass |RS| = |PQ| und RS || PQ gilt.
Ich weiß, dass ich damit beginnen muss, mit dem Radius des Kreises k jeweils einen Kreis um den Punkt P und einen Kreis und den Punkt Q machen muss. Aber an welchen der beiden Schnittpunkte der Kreise muss ich dann Verschieben und wieso?
Ich hoffe jemand kann mir helfen. Danke schon mal im Voraus!