Bestimmen Sie den Wert von z so, dass der Extrempunkt von Yz auf dem Graphen F liegt.

Question

Aufgabe: Bestimmen Sie den Wert von z so, dass der Extrempunkt von Yz auf dem Graphen F liegt.

Problem/Ansatz:

Yz= z*x(x-3) Hochpunkt liegt bei (1,5|4,5) aus der vorherigen Aufgabe

F=-1/3x^3+3

Ich weiß hab nicht wirklich einen Plan wie ich dass jetzt ausrechnen soll und was ich machen muss, hab so eine Aufgabe das erste mal

Answer 1

Willkommen in der Mathelounge,

der Hochpunkt hat die Koordinaten H (1,5|-2,25z). Wie kommst du auf 4,5?

Setze 1,5 in die Gleichung von f ein.

\(f(1,5)=-\frac{1}{3}\cdot 1,5^3+3=\frac{15}{8}\)

Setze diese y-Koordinate = -2,25 z und löse nach z auf:

\(\frac{15}{8}=-\frac{9}{4}z\\ -\frac{5}{6}=z\)

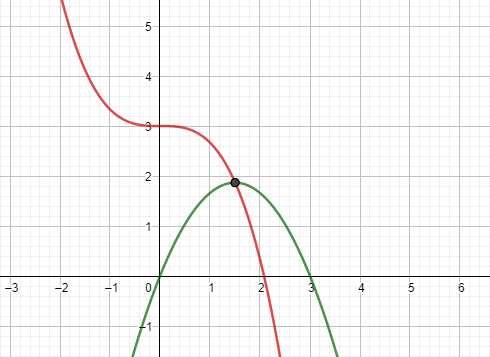
Melde dich, falls du dazu noch Fragen hast.

Gruß, Silvia

Comments

Hey danke schonmal für deine schnelle Antwort, ich habe anscheinend irgendetwas falsch geschrieben, dass sind die beiden Funktionen:

und dazu war jetzt halt die Aufgabenstellung. die g(x)=Yz(x) war vorher z*x*(x-3) aber in der Aufgabe davor sollte man für z=-2 einsetzen und dann kam wie oben im Bild gezeigt dass raus, mit dieser Funktion (-2x^2+6x) sollen wir weiterrechnen, also entschuldige falls ich etwas verpeilt habe. LG Anna

---

Hallo Anna,

In der Funktion g ist aber jetzt kein z mehr vorhanden. Also denke ich, dass du mit der ursprünglichen Funktion \(Y_z(x)\) rechnen solltest.

---

Mhh ich glaube nicht, ich hab die Lösungen hier und es soll für z= -1,5 rauskommen :/

---

Kannst du mal die genaue Aufgabenstellung fotografieren und einstellen?

---

Ich glaube dass ist verboten wenn ich dass hier komplett reinstelle würde, hast du eine email oder so wo ich es dir schicken könnte? Wäre toll:)

---

ich hab die Lösungen hier und es soll für z= -1,5 rauskommen

was korrekt ist! Wenn $$Y_z(x)= zx(x-3)$$dann ist $$g(x)=Y_{(z=-2)}(x)=-2x(x-3) = -2x^2 + 6x$$und das Extremum von \(Y_z(x)\) ist unabhängig von \(z\) und \(x_e=1,5\). Einsetzen in \(F\) alias \(f(x)\) gibt$$f(1,5)= -\frac13(1,5)^3+3\cdot 1,5 = \frac{27}8 = 3,375$$das als \(g(x_e=1,5)\) einsetzen$$g(1,5)=\frac{27}8 =- z \cdot \left(\frac 32\right)^2 = -\frac 94 z \implies z = -\frac 32$$

---

@Werner - Danke, das schaue ich mir nochmal in Ruhe an

@Anna - Dann brauchst du meine Mailadresse ja nicht mehr, aber sie steht in meinem Profil

---

hab es jetzt verstanden vielen Dank:)