Aufgabe:
Die Zufallsvariable X hat eine stückweise konstante Dichtefunktion f.
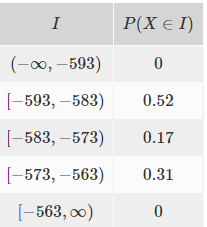
Diese ist gegeben durch die folgende Tabelle, welche die Wahrscheinlichkeiten für jene Intervalle enthält, in denen f konstant ist.
Text erkannt:
\begin{tabular}{c|c}
\( I \) & \( P(X \in I) \) \\
\hline\( (-\infty,-593) \) & 0 \\
\hline\( [-593,-583) \) & \( 0.52 \) \\
\hline\( [-583,-573) \) & \( 0.17 \) \\
\hline\( [-573,-563) \) & \( 0.31 \) \\
\hline\( [-563, \infty) \) & 0 \\
\hline
\end{tabular}
Berechnen Sie die Wahrscheinlichkeit P(−590<X<−565).
Problem/Ansatz:
ich habe die Intervalle, die mit dazu gehören berechnet und komme so auf:
((-583) - (-593)) * 0,52 + ((-573) - (-583)) * 0,17 + ((-563) - (-573)) * 0,31 = 10
das ist aber Murks, da ja eine Zahl zwischen 0 und 1 herauskommen sollt, da es hier um eine Wahrscheinlichkeit geht...
Dieser Lösungsweg hat sonst allerdings geklappt, das einzige, was mir auffällt, ist, dass hier die Wahrscheinlichkeiten größer sind.