Winkelhalbierende und Mittenparallele konstruieren

Question

(a) Konstruieren Sie mit Zirkel und Lineal die Winkelhalbierende eines vorgegebenen Win- kels. Verwenden Sie dabei so wenig Schritte wie möglich und weisen Sie die Richtigkeit Ihrer Konstruktion nach.
(b) Konstruieren Sie mit Zirkel und Lineal die Mittenparallele zweier paralleler Geraden (also die Gerade, die zu den beiden vorgegebenen Geraden parallel ist und von beiden Geraden den gleichen Abstand hat). Verwenden Sie dabei so wenig Schritte wie möglich und weisen Sie die Richtigkeit Ihrer Konstruktion nach.

Answer 1

a)

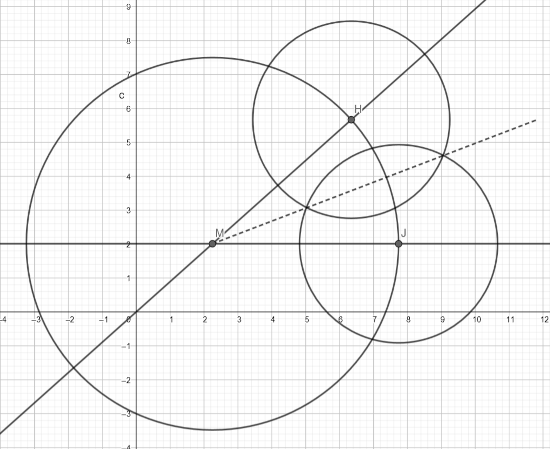
- um die Spitze des Winkels M einen Kreis zeichnen

- um die Schnittpunkte H und J dieses Kreises mit dem Schenkeln des Winkels zwei weitere Kreise mit identischem Radius zeichnen

- Schnittpunkte der Kreise verbinden (Winkelhalbierende)

b)

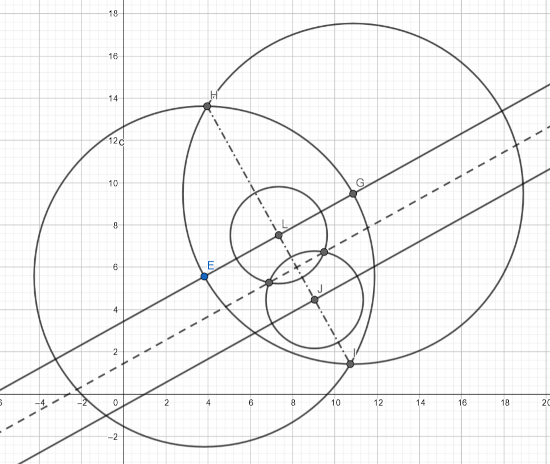
- um einen belibigem Punkt E auf einer Geraden einen Kreis zeichnen

- um den Schnittpunkt G Kreis mit identischem Radius zeichnen

- die Gerade durch die Schnittpunkte H und I bilden die Senkrechte der parallelen Geraden

- um L und J Kreise mit identischem Radius zeichnen

- die Gerade durch die Kreisschnittpunkte ist die Mittelparallele

Answer 2

a) S sei der Scheitel des Winkel, \( \vec{a} \) und \( \vec{b} \) seien seine Schenkel. Ein Kreis um S mit beliebigem Radius scheidet die Schenkel in A und in B, Die Kreise um A und B mit gleichem Radius schneiden sich auf der Winkelhalbierenden. Nachweis mit Spiegelung eines Schenkels an der Winkelhalbierenden.

b) g und h seien parallele Geraden, P sei ein Punkt auf g. Das Lot auf g in P schneidet h in Q. Die Kreise mit gleichem Radius um P und um Q schneiden sich auf der Mittelparallelen. Nachweis mit Spiegelung von g an der Mittelparallelen.