Kommt drauf an, wie viel du zu Kurvendiskussionen bereits gelernt hast. g(x) = 1/x solltest du unbedingt genau kennen. bei f(x) handelt es sich um eine verschobene Version von g(x)
Ein Funktionsplot hilft immer:
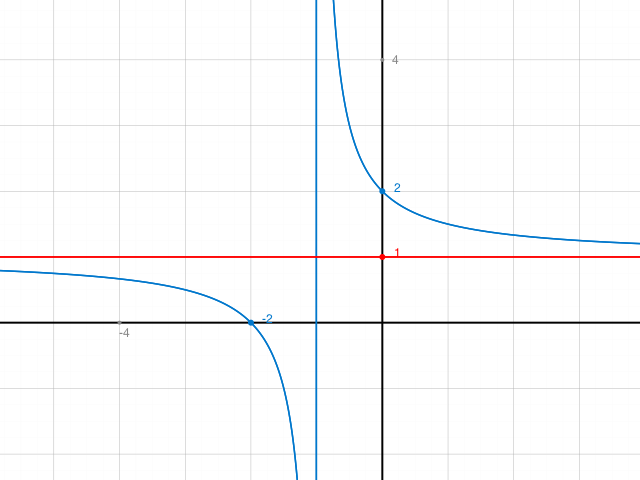
Aus der Funktionsgleichung kann man ablesen:
f(x) = (x+2)/(x+1)
hat bei x=-1 ein Polstelle.
und y=1 ist eine horizontale Tangente an f(x).
Schreibe f(x) = (x+2)/(x+1) = (x+1+1)/(x+1) = 1 + 1/(x+1)
Nun ist klar, dass y= 1 nicht erreicht wird. W(f) = {x|x Element R, x≠1}
Alternative: y =(x+2)/(x+1) nach y auflösen und Definitionsbereich der Umkehrfunktion untersuchen.
y =(x+2)/(x+1) |x≠1
y= 1+1/(x+1)
y-1 = 1/(x+1) |zusätzlich y≠1,
(da der Bruch rechts nie genau 0 geben kann, kann y nicht 1 sein)
(x+1) = 1/(y-1)
x= -1 + 1/(y-1) |für y≠1
Hier sind die Bedingungen für Äquivalenzumformungen nicht erfüllt. Man muss gut aufpassen und hinschreiben, welche weiteren Voraussetzungen dazukommen. Allenfalls Fallunterscheidungen nötig. Benutze diese Methode nur, wenn du mit der Kurvendiskussion nirgends hinkommst.