In ein Quadrat der Seitenlänge a=10cm sind fünf Kreise eingezeichnet. Flächeninhalt?

Question

In ein Quadrat der Seitenlänge a=10cm sind fünf Kreise wie folgt eingezeichnet:

Der mittelkreis hat den Schnittpunkt der diagonalen des Quadrats als Mittelpunkt :

die vier großen eckkreise berühren den inneren Kreis sowie zwei Seiten des Quadrats:

in der Mitte mit fünf gleich großen kreisen:

in den rechts mit maximalen großen mittelkreis!

Berechne den Anteil der Fläche des Quadrats die von den Kreisen überdeckt wird!

Präzision: Es sind 2 Aufgaben 

Es ist ein Kreis immer genau in der Mitte angeordnet und der Rest in den Ecken,
bei der ersten Aufgabe sind alle gleichgroß
bei der zweiten ist der in der Mitte am größten und der Rest klein. Es ist aber so groß wie möglich. Also noch größer geht der Kreis in der Mitte nicht!

Comments

Frage :

  - sind die Kreise nun gleichgroß

  oder

  -  habe ich 4 gleichgroße Eckkreise ( d  = 5 cm ) und in der Mitte
     den passenden Mittelkreis

  Falls wortmäßig nicht zu klären dann bitte eine Skizze.

  mfg Georg

---

Also der in der Mitte da sind sowohl die eckkreise als auch der Kreis in der Mitte gleich groß! Rechts ist der Kreis in der Mitte am größtmöglichen und die eckkreise sind sehr klein, leider kann ich meine Skizze machen weil ich von Handy her antworte

---

sind das 2 Aufgaben ? mit unterschiedlicher Kreisanordnung ?

- sind das 5 gleichgroße Kreise

- oder 4 maximal große Eckreise mit 1 kleinem Kreis in der Mitte

- oder 1 maximal großer Kreis in der Mitte und 4 kleine Eckkreise ?

  mfg Georg

---

Ja 2 aufgaben Es ist ein Kreis immer genau in der Mitte angeordnet und der Rest in den Ecken, bei der ersten Aufgabe sind alle gleichgroß bei der zweiten ist der in der Mitte am größten und der Rest klein es ist aber so groß wie möglich also noch größer geht der Kreis in der Mitte nicht!

Answer 1

Wenn ich es richtig verstanden habe, soll das erste Quadrat so aussehen: 

 

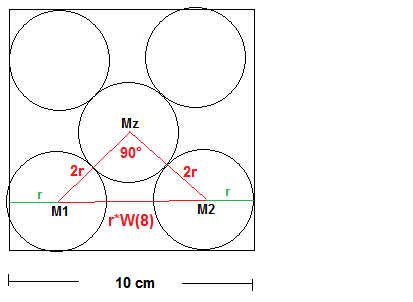
Alle Kreise sind gleich groß und haben den Radius r. Die Mittelpunkte der Randkreise liegen auf jeweils einer der Diagonalen des Quadrates, der Mittelpunkt des Zentralkreises liegt sogar auf beiden Diagonalen, ist also identisch mit deren Schnittpunkt.

Da sich die Diagonalen eines Quadrates im rechten Winkel schneiden, ist das Dreieck M1MzM2 rechtwinklig. 

Für den Abstand M1Mz sowie MzM2 gilt:

M1Mz = MzM2 = 2 r  

Wegen der Rechtwinkligkeit gilt für die Strecke M1M2 nach Pythagoras:

M1M2 = √ ( ( 2 r ) ² + ( 2 r ) ² ) = √ ( 8 r ² ) = r * √ 8

Außerdem gilt, wie man der Skizze entnehmen kann:

M1M2 + 2 r = 10

<=> r * √ 8 + 2 r = 10

<=> r ( 2 + √ 8 ) = 10

<=> r = 10 / ( 2 + √ 8 )

Nun kennt man den Radius r der 5 Kreise und kann deren gesamten Flächeninhalt A_ges  berechnen:

A_ges = 5 * π * r ²

= 5 * π * (10 / ( 2 + √ 8 ) ) ² ≈ 67,38 cm ²

Da das Quadrat einen Flächeninhalt von A_Q = 100 cm ² hat, überdecken die 5 Kreise also

67,38 / 100 = 0,6738 = 67,38 %

des Flächeninhaltes des Quadrates.

 

Quadrat 2 sieht wohl so aus:

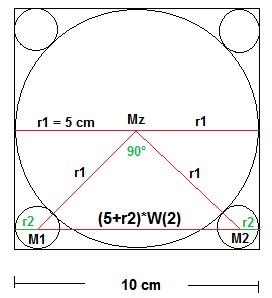
Auch hier liegen die Kreismittelpunkte auf den Diagonalen des Quadrats, sodass also auch hier das Dreieck M1MzM2 rechtwinklig ist.

Für den Radius r₁ des großen Kreises gilt:

r₁ = 5 cm

Sei nun r₂ der Radius der kleinen Kreise. Dann gilt nach Pythagoras für die Strecke M1M2:

( M1M2 ) ² = ( r₁ + r₂ ) ² + ( r₁ + r₂ ) ² = 2 ( 5 + r₂ ) ²

<=> M1M2 = √ ( 2 ) * ( 5 + r₂ )

Außerdem gilt, wie man der Skizze entnehmen kann:

M1M2 + 2 * r₂ = 10

<=> M1M2 = 10 - 2 * r₂

Aus den fett gesetzten Gleichungen folgt nun:

10 - 2 * r₂ = √ ( 2 ) * ( 5 + r₂ ) = √ ( 2 ) * 5 + √ ( 2 ) * r₂

Auflösen nach r₂ :

<=> 10 - 5 * √ ( 2 ) = 2 * r₂ + √ ( 2 ) * r₂ = r₂ * ( 2 + √ 2 )

<=> r₂ = ( 10 - 5 * √ ( 2 ) ) / ( 2 + √ 2 )

<=> r₂ ≈ 0,858 cm

Der gesamte Flächeninhalt A_ges der 5 Kreise beträgt daher:

A_ges = pi * r₁ ²  + 4 * pi * r₂ ²

= pi * ( 5 ² + 4 * 0,858 ² )

= 87,79 cm²

Da das Quadrat einen Flächeninhalt von A_Q = 100 cm ² hat, überdecken die 5 Kreise also:

87,79 / 100 = 0,8779 = 87,79 %

des Flächeninhaltes des Quadrates.

Comments

Hi JotEs ich sitze jetzt am Pc und vielen Dank für deine ausführliche Antwort. Allerdings verstehe ich in aufgabe 2 leider nicht diese Umstellung wo bleibt die 10-2*r2? 

 

Aus den fett gesetzten Gleichungen folgt nun:

10 - 2 * r2 = √ ( 2 ) * ( 5 + r2 ) = √ ( 2 ) * 5 + √ ( 2 ) * r2 -> wo ist hier 10-2*r2

Auflösen nach r2 :

<=> 10 - 5 * √ ( 2 ) = 2 * r2 + √ ( 2 ) * r2 = r2 * ( 2 + √ 2 )

<=> r2 = ( 10 - 5 * √ ( 2 ) ) / ( 2 + √ 2 )

<=> r2 ≈ 0,858 cm

---

Sieh das mal so, wenn es dir dann leichter fällt:

10 - 2 * r₂ = √ ( 2 ) * ( 5 + r₂ )

10 - 2 * r₂ = √ ( 2 ) * 5 + √ ( 2 ) * r₂

---

das auflösen von r2 verstehe ich auch nicht schreib mal bitte hinter einem strich was du minus oder plus zu anderen seite nimmst

---

Das ist das auflösen einer linearen Gleichung. Also nichts weltbewegendes

10 - 2 * r₂ = √ ( 2 ) * 5 + √ ( 2 ) * r₂

Ich schreibe das nur mal etwas kompakter

10 - 2·r = √2·5 + √2·r   | + 2·r - √2·5

10 - √2·5 =  2·r + √2·r   | r ausklammern

10 - √2·5 =  (2 + √2)·r   | : (2 + √2)

r = (10 - √2·5) / (2 + √2)

TR zücken und ausrechnen.
 

---

Ich schreibe den Absatz mal ohne Gleichungsketten, dafür mit mehreren Gleichungen, die ich im Einzelnen erläutere:

 

Aus den fett gesetzten Gleichungen folgt nun:

10 - 2 * r2 = √ ( 2 ) * ( 5 + r2 )

Ausmultiplizieren der rechten Seite:

<=> 10 - 2 * r2 = √ ( 2 ) * 5 + √ ( 2 ) * r2

Auflösen nach r2:
Dazu auf beiden Seiten 5 * √ ( 2 ) subtrahieren:

<=> 10 - 2 * r2 - 5 * √ ( 2 ) = √ ( 2 ) * r2

dann auf beiden Seiten  2 * r2 addieren:

<=> 10 - 5 * √ ( 2 ) = √ ( 2 ) * r2  + 2 * r2

Auf der rechten Seite r2 ausklammern:

<=> 10 - 5 * √ ( 2 ) = r2 * ( 2 + √ 2 )

beide Seiten durch ( 2 + √ 2 ) dividieren:

<=> ( 10 - 5 * √ ( 2 ) ) / ( 2 + √ 2 ) = r2

Umstellen und ausrechnen:

<=> r2 ≈ 0,858 cm

Answer 2

Bei 5 gleich großen Kreisen mit dem Radius 1

5·pi·1^2 / (4·SIN(45°) + 2)^2 = 0.6737651055 = 67.38%

Es werden ca. 67.38% der Quadratfläche überdeckt.


Für einen maximal großen Innkreis mit dem Radius 1

(1 + r)·SIN(45°) + r = 1
r = 3 - 2·√2

(pi·1^2 + 4·pi·(3 - 2·√2)^2) / 2^2 = 0.8778780165 = 87.79%

Es werden ca. 87.79% der Quadratfläche überdeckt.


Wichtig für Dich. Zeichne dir eine Skizze. Auch ich habe für meine Überlegungen gerade eine Skizze gemacht. Und dann versuche meine Rechnungen nachzuvollziehen.