Welche Fläche verdeckt das unbewegliche Unterteil?

Question

Aufgabe: Eine Apparatur hat eine Blende in Form einer Parabel ݂f(x)= 1/2x².
Die Blende ist 4 LE breit (Achsen sind auf 1 LE normiert). Ihr Unterteil ist unbeweglich.
a) Welche Fläche verdeckt das unbewegliche Unterteil?
b) Der Oberteil der Blende wird um 1 LE in Richtung der positiven y-Achse verschoben.
Welche Fläche hat der entstehende Spalt zwischen Unter- und Oberteil

Problem/Ansatz: Ich weiß leider nicht wie ich anfangen soll, habe mir darüber jetzt schon sehr lange den Kopf zerbrochen aber komme immer auf kein Ergebnis

Comments

War vielleicht bei der Aufgabe eine Skizze dabei. Ansonsten habe ich Schwierigkeiten mir das vorzustellen.

---

Ja, es gibt eine Skizze

Answer 1

Hallo,

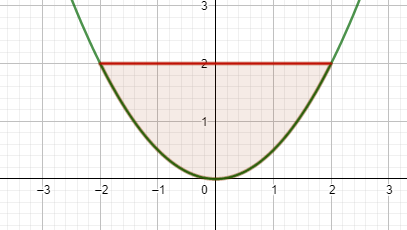
für den Unterteil berechnest du das Integral zwischen den Funktionen f(x) und y = 2.

f(x) um eine Einheit nach oben verschoben ergibt die Funktion \(g=3\)

Berechne das Integral zwischen f und g und ziehe davon dein Ergebnis aus a) ab.

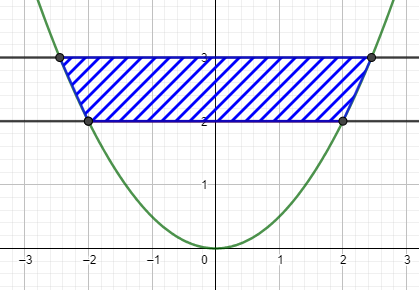
Zur Kontrolle kannst du auch die Trapezfläche berechnen.

Gruß, Silvia

Comments

Meine Interpretation :

---

Ich habe die Striche übersehen/ignoriert/nicht beachtet und daher wird deine Interpretion richtig sein. Wäre ja auch erstaunlich, wenn es anders wäre. ;-)

---

Welche Fläche hat der entstehende Spalt zwischen Unter- und Oberteil

Weil dort etwas von Spalt zwischen Obre- und Unterteil steht würde ich mir das evtl. so vorstellen. Allerdings wäre das ja viel zu einfach zu berechnen.