Question

Von 3 gleich langen Streichhölzchen wird eines verkürzt. Wer das verkürzte Hölzchen verdeckt zieht, hat verloren.

Wie könnte zu diesem Zufallsversuch ein beschriftetes Baumdiagramm aussehen?

Gruß Ommel

Comments

1. Ziehen Wahrscheinlichkeit 1/3 für verkürzt,  2/3 für lang

2. Ziehen, man geht davon aus, dass beim 1. Ziehen das verkürzte Hölzchen gezogen wurde, und nun sind nur noch 2 Hölzchen da.

   Wahrscheinlichkeit 1/2 für verkürzt,   1/2  für lang

3. Ziehen, man geht davon aus, dass beim 2. Ziehen das verkürzte Hölzchen gezogen wurde

    Wahrscheinlichkeit 1/1 für verkürzt , es ist ja auch nur noch das eine Hölzchen da

Jetzt kommt überall 1/3 als Wahrscheinlichkeit raus, wenn man die Pfade multipliziert:

beim 1.Ziehen 1/3

beim 2.Ziehen 2/3 *1/2 = 1/3

beim 3.Ziehen 2/3 *1/2 *1 = 1/3

......oder irre ich mich da?

Schöne Grüße von Ommel

---

... oder malt man da nur die 1. Stufe auf:

ein Pfad geht zu 'langes Hölzchen' = 2/3 Wahrscheinlichkeit

und der andere Pfad geht zu 'verkürztes Hölzchen' = 1/3 Wahrscheinlichkeit.

Reicht das dann schon?

Gruß Ommel

Answer 1

Wie viele Personen ziehen denn ein Hölzchen ?

Davon hängt die Anzahl der Stufen des Baumdiagramms ab.

Zieht eine Person hat man eine Stufe, ziehen zwei Personen hat man zwei Stufen und ziehen sogar drei Personen hat man drei Stufen.

Wird sogar mit zurücklegen gezogen dann könnten sogar noch mehr Personen ziehen und das Baumdiagramm wird entsprechend um mehr Stufen erweitert.

Comments

Das steht leider nicht in der Aufgabenstellung. Da heißt es so:

'Ein mögliches Losverfahren ist das "Ziehen von Streichhölzchen.

 Von  drei  gleichen Streichhölzern wird eines verkürzt.

Derjenige, der verdeckt das kurze Hölzchen zieht, hat verloren.

a) Zeichnen Sie zu diesem Zufallsversuch ein beschriftetes Baumdiagramm. '

---

Ich würde annehmen das drei Leute dann ziehen. Und es ohne Zurücklegen gezogen wird.

Answer 2

Salut ommel,

vielleicht hilft dir diese Skizze weiter:

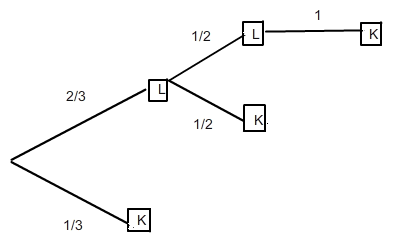
Kurze Interpretation:

Die Wahrscheinlichkeit, dass das kurze Streichholz gezogen wird, beträgt 1/3.

Wird beim 1. Ziehen eines der langen Streichhölzer gezogen, hast du dann ja noch 2 Streichhölzer übrig. Die Wahrscheinlichkeit, dass nun das kurze Streichholz gezogen wird, beträgt 1/2.

Du musst aber noch die Einzelwahrscheinlichkeiten entlang des Pfades multiplizieren:

2/3 * 1/2 = 1/3

Die Wahrscheinlichkeit somit, das kurze Streichholz zu ziehen, beträgt erneut 1/3.

Zwei lange Streichhölzer wurden also bis jetzt gezogen, das kurze Hölzchen ist noch vorhanden, dh. die Wahrscheinlichkeit, dieses Streichholz zu erwischen, beträgt 1.

Wieder die Einzelwahrscheinlichkeiten entlang des Pfades multiplizieren:

2/3 * 1/2 * 1 = 1/3

Die Wahrscheinlichkeit schlussendlich, das kurze Streichholz zu ziehen, beträgt erneut 1/3.

Viel Erfolg ;).