Funktionsgleichung durch gegebenen Hoch- und Tiefpunkt

Question

Wie heisst die Funktion zum Graphen mit dem Hochpunkt H(1/0) und dem Tiefpunkt T(-1/0)?

Answer 1

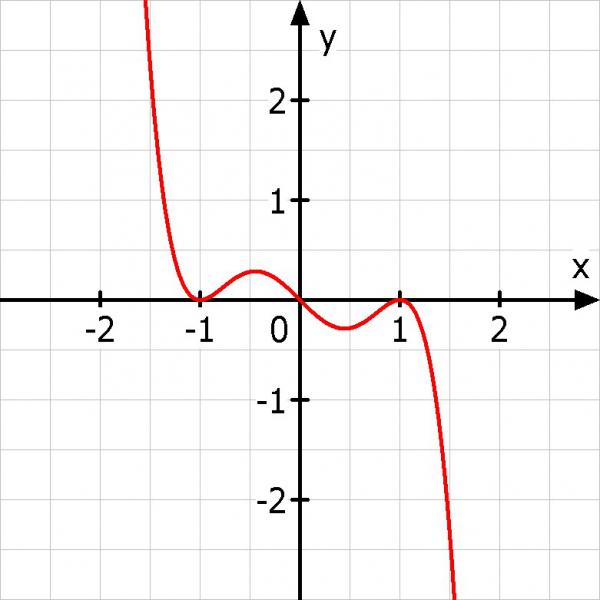
Wir brauchen eine doppelte Nullstelle bei -1 und eine doppelte Nullstelle bei +1 außerdem noch eine einfache Nullstelle bei 0.

Also vermute ich eine Funktion

f(x) = -x * (x+1)² * (x-1)²
f(x) = -x * (x² + 2x + 1) * (x² - 2x + 1)
f(x) = -x * (x⁴ - 2x³ + x² + 2x³ - 4x² + 2x + x² - 2x + 1)
f(x) = -x * (x⁴ - 2x² + 1)
f(x) = -x⁵ + 2x³ - x

 

Ach ich war hier etwas ungeschickt. Man hätte auch die 3. binomische Formel zum ausmultiplizieren benutzen können.

Hier zeichne ich noch den Graphen:

Comments

Es gibt allerdings unendlich viele Graphen die diese Bedingungen erfüllen. ich habe hier jetzt nur mal eine der einfachsten genommen.

Man könnte diese Funktion aber auch mit einem beliebigen positiven Faktor a multiplizieren und hat ebenso eine Funktion, die die Bedingungen erfüllt. Ebenso wäre eine Funktion denkbar die den weiteren Nulldurchgang nicht genau im Koordinatenursprung hat.

Wenn also keine weiteren Einschränkungen gemacht werden, kann man sich für eine Funktion die die Bedingungen erfüllt entscheiden.

---

1. Wie komme ich von dieser gstellten Aufgabe analytisch auf die Feststellung: "Wir brauchen eine doppelte Nullstelle bei -1 und eine doppelte Nullstelle bei +1, außerdem noch eine einfache Nullstelle bei 0."?

2.Mit welcher Technik komme ich von dem, was man braucht (siehe oben) auf die Vermutung der angegebenen Funktion?

3. Was ist eine "doppelte" Nullstelle?

---

vgl. auch meinen Kommentar bei der Aufgaben zum Minimum.

Dort hat es sich übrigens rausgestellt, dass Funktionen vom Typ f(x) = ax hoch3 + bx hoch 2 + cx + d bekannt sind.

---

Bei eine einfachen Nullstelle schneidet der Graph die x-Achse. Bei einer doppelten Nullstelle berührt er nur die x-Achse liefert also einen Hoch oder Tiefpunkt.

Das was du weißt sieht also etwa so aus:

Nun ist die Frage wie wir die beiden Funktionsgraphen zwischen den Extrempunkten stetig verbinden können. Das einzige was dort machbar ist, wenn der Graph nochmal die x-Achse schneidet. Das nehme ich also der einfachheit halber mal bei x = 0 an.

Den Schnittpunkt mit der x-Achse liefert am einfachsten eine einfache Nullstelle.

 

---

Nett ist auch die Lösung

-(x-1)²*(x+1)²/x