Definiton absoluter Tiefpunkt/Hochpunkt

Question

Aufgabe:

Notwendiges Kriterium für einen absoluten Hoch oder Tiefpunkt.

In meinem Heft steht: Dass bei absoluten Hoch oder Tiefpunkten keine waagerechte Tangente vorliegen brauch, falls sich dieser Punkt wie in unserem Beispiel am Ende des betrachteten Intervalls befindet.

Weiter erfüllt ja ein Randextremum am Ende eines Intervalls ja auch die Bedingung das er der Extremste Punkt in seiner Umgebung ist. Also sollte es ein absoluter und relativer Extrempunkt sein. (So steht es auch auf einigen Seiten im Internet). Jetzt steht auf der nächsten Seite aber das Kriterium f'(x)=0 ist notwendig für einen relativen Hoch oder Tiefpunkt. Das wiederspricht ja aber der Aussge das keine waagerechte Tangente vorliegen muss. Ich habe einmal eine Skizze des Graphen gezeichnet. Es handelt sich um den letzten Punkt mit der Beschriftung a.T und r.T.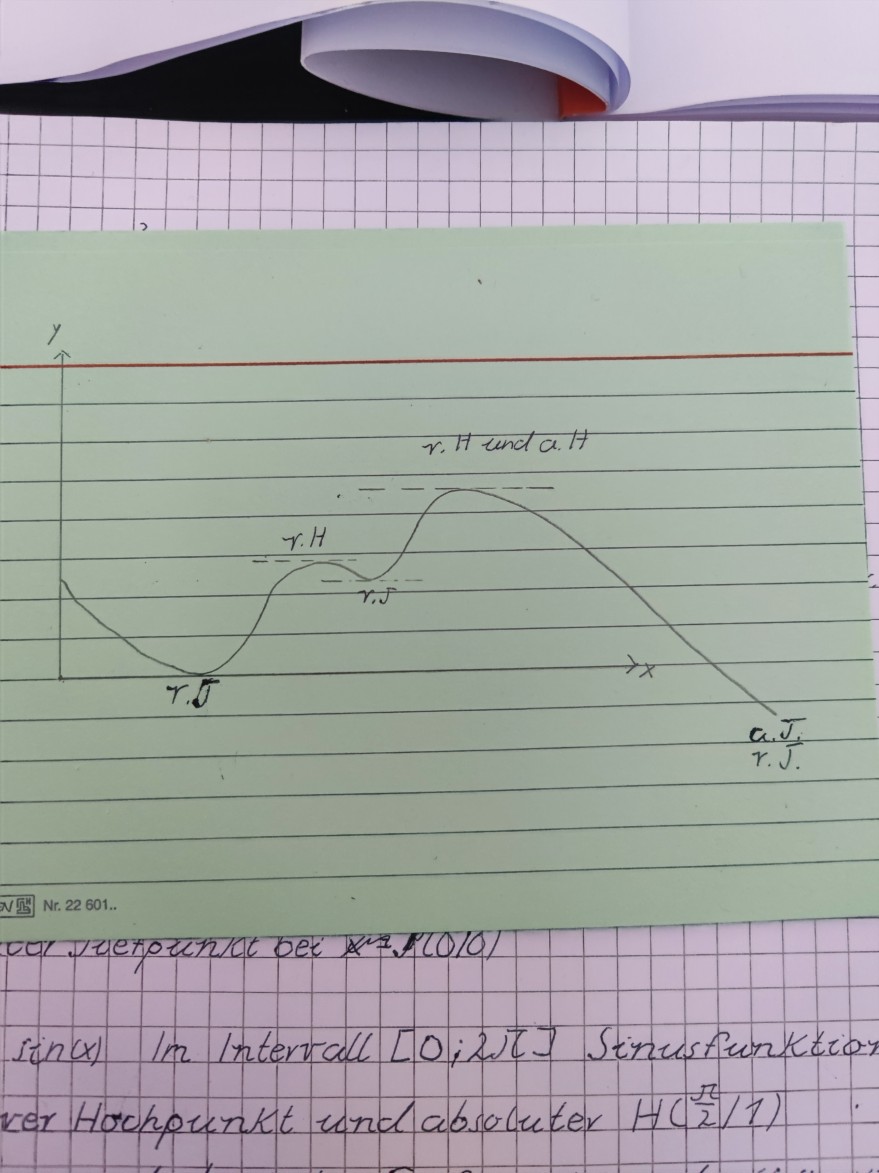

Text erkannt:

Comments

Entweder ist die Definiton der Umgebung hier nicht klar dargestellt oder ich weiss es auch nicht. Der letzte Punkt der als absoluter Tiefpunkt dargestellt ist, müsste auch ein relativer sein ( mit einer Steigung ungleich 0.) . Denn die Umgebung U ist nicht definiert als links und rechtsseitige Umgebung, auch wenn man sich das denken könnte. Das wiederspricht dann aber zum Beispiel diesem Bild Ausschnitt von Mathe Guru wo jeder absolute Hoch und Tiefpunkt auch ein relativer ist, auch das Randextremum.

https://matheguru.com/differentialrechnung/extremstellen-extrempunkte.html siehe erste Zeichnung

Answer 1

Ich habe mal eine Zeichnung zur Klärung erstellt:

Comments

Dankeschön. Also sind die Randexttrempunkte keine relativen (lokalen) Extrempunkte?

---

Bei meiner gewählten Funktion ist es so.

Es sind aber auch Funktionen denkbar, wo Randextrema auch waagerechte Tangenten besitzen.