Aufgabe:
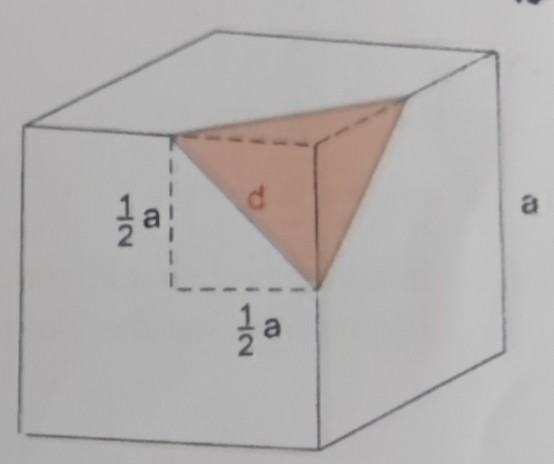
Von einem Würfel der Kantenlänge \( a=5 \mathrm{~cm} \) wird eine Ecke abgeschnitten. Dabei trifft der Schnitt die entsprechenden Würfelkanten in ihrer Mitte. Die in Abb. \( 1.31 \) rot dargestellte Schnittfläche ist also ein gleichseitiges Dreieck. Wie groß ist seine Fläche?
Mit den erwähnten Formeln ist eine Lösung schnell durchgeführt:
- Aus der Formel für die Diagonale in einem Quadrat lässt sich die Seitenlänged des gleichseitigen Dreiecks berechnen, wenn man ein Quadrat mit der halben Kantenlänge des Würfels zu Grunde legt. Es gilt:
\( \mathrm{d}=\frac{1}{2} \cdot \mathrm{a} \cdot \sqrt{2} \)
Einsetzen dieses Terms in die Flächenformel für das gleichseitige Dreieck ergibt dann:
\( \mathrm{A}=\frac{1}{4} \cdot\left(\frac{1}{2} \cdot \mathrm{a} \cdot \sqrt{2}\right)^{2} \cdot \sqrt{3} \)
Auflösen der Klammer (Vorsicht, drei Faktoren!) und Zusammenfassen liefert:
\( \mathrm{A}=\frac{1}{4} \cdot \frac{1}{4} \cdot \mathrm{a}^{2} \cdot 2 \cdot \sqrt{3}=\frac{1}{8} \cdot \mathrm{a}^{2} \cdot \sqrt{3} \)
Einsetzen von \( \mathrm{a}=5 \) ergibt den gesuchten Flächeninhalt \( \mathrm{zu} \mathrm{A} \approx 5,413 \mathrm{~cm}^{2} \).
Mit diesem Beispiel soll die Behandlung der Satzgruppe des Pythagoras abgeschlossen werden. Bitte beachten Sie bei der Bearbeitung des nachfolgenden Aufgabenblocks, dass die Anwendungen des Pythagoras-Satzes ungeheuer vielfältig sind. Daher fällt dieser Aufgabenblock etwas umfangreicher aus. Bitte versuchen Sie, die hier gestellten Aufgaben vollständig zu lösen und achten Sie dabei auf den mathematisch korrekten Umgang mit den auftretenden Termen. Denken Sie daran, dass in diesem Sachzusammenhang auch einmal eine quadratische Gleichung auftreten kann!
Problem/Ansatz:
Die Seitenlänge der Dreiecks ist gleich der Diagonalen aus dem Quadrat von (1/2a)^2.
Im Buch steht für die Diagonale die Lösung: d= (1/2)*a*Wurzel2
Ich komme aber auf Wurzel(1/2)*a
Weg: d^2= (1/2a)^2+(1/2a)^2
d^2= 1/4a^2+1/4a^2
d^2 = 1/2a^2 | wurzel
d = Wurzel(1/2)*a
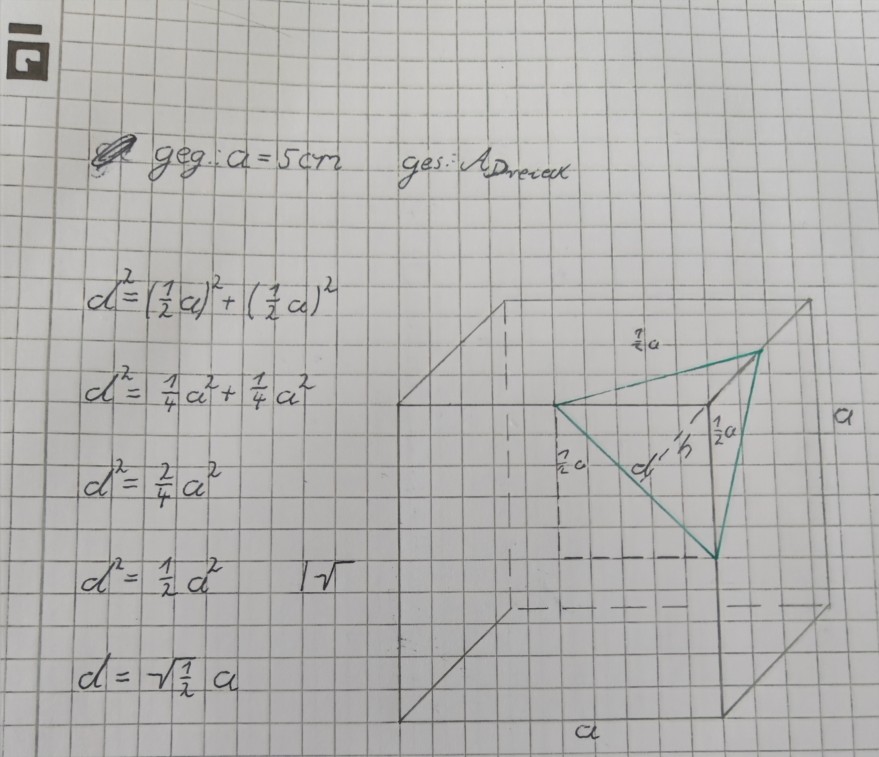
geg: \( a=5 \mathrm{~cm} \) ges. \( A_{\text {reied }} \)
\( \begin{array}{l} d^{2}=\left(\frac{1}{2} a\right)^{2}+\left(\frac{1}{2} a\right)^{2} \\ d^{2}=\frac{1}{4} a^{2}+\frac{1}{4} a^{2} \\ d^{2}=\frac{2}{4} a^{2} \\ d^{2}=\frac{1}{2} a^{2} \quad \sqrt{ } \\ d=\sqrt{\frac{1}{2}} a \end{array} \)